Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 29.Problemas Adicionais - Ex. 72
Na figura 29-76, uma espira conduz uma corrente . A espira é formada por ois segmentos radiais e dois arcos de circunferência concêntrica de raios e . O ângulo é . Determine (a) o módulo e (b) o sentido (para dentro ou para fora de papel) do campo magnético no centro de curvatura .
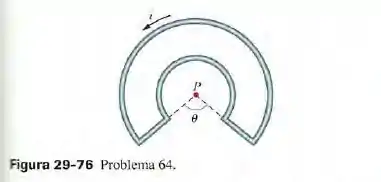
Passo 1
Para descobrirmos o campo magnético no ponto P podemos fazer o cálculo por trechos do objeto em questão. Vamos iniciar olhando as partes retilíneas. A lei de Biot-Savart nos diz o seguinte:
Para os dois elementos retilíneos, o ângulo entre é zero e . Portanto:
Assim, a contribuição de toda a parte reta para o campo magnético é zero.
Passo 2
Usando o vetor unitario para indicar a direção “para fora do papel”, temos:
O que nos dá .
O sentido é , ou seja, para dentro do papel.
Resposta
- ;
- O sentido é , ou seja, para dentro do papel.