Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 31.10 - Ex. 61

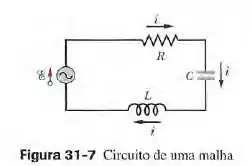
Na figura 31-7, R = 15,0   Ω , C = 4,70   μ F e L = 25,0   m H . O gerador produ uma força eletromotriz com uma tensão rms de 75,0   V e uma frequência de 550   H z . (a) Qual é a corrente rms? Determine a tensão rms (b) em R ; (c) em C ; (d) em L ; (e) em C e L juntos; (f) em R ,   C   e   L juntos. Determine a potência média dissipada (g) em R ; (h) em C ; (i) em L .

Passo 1

Bom, galera, a corrente rms é igual a:

I r m s = ε r m s Z

I r m s = ε r m s R 2 + 2 π f L - 1 2 π f C 2  

I r m s = 75,0   V √ ( 15,0   Ω 2 + 2 π 550   H z 25,0   m H - 1 2 π 550   H z 4,70   μ F ²

I r m s = 2,59   A

Passo 2

A tensão rms em R é dada por:

V r m s = I r m s R

V r m s = 2,59   A 15,0   Ω

V r m s = 38,8   V

Passo 3

A tensão rms em C é dada por:

V r m s C = I r m s X C = I r m s 2 π f C

V r m s C = 2,59   A 2 π 550   H z 4,70   μ F

V r m s C = 159   V

Passo 4

A tensão rms em L é dada por:

V r m s L = I r m s X L = 2 π I r m s f L

V r m s L = 2 π 2,59   A 550   H z 25,0   m H

V r m s L = 224   V

Passo 5

A tensão rms em C e L juntos é:

V C L = V r m s C - V r m s L

V C L = 159,5   V - 223,7   V

V C L = 64,2   V

Passo 6

A tensão rms em R ,   C   e   L juntos é:

V R C L = V r m s 2 + V C L 2

V R C L = 38,8 2 + 64,2 2

V R C L = 75,0   V

Passo 7

A potência média dissipada em R é:

P R = V r m s 2 R

P R = 38,8   V 2 15,0   Ω

P R = 100   W

Passo 8

As potências no capacitor e no indutor são iguais a zero.

Resposta

  1. I r m s = 2,59   A ;
  2. V r m s = 38,8   V ;
  3. V r m s C = 159 V ;
  4. V r m s L = 224 V ;
  5. V C L = 64,2   V ;
  6. V R C L = 75,0   V ;
  7. P R = 100   W ;
  8. P C = 0 ;
  9. P L = 0 .
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um resistor e um capacitor estão conectados em paralelo com um gerador ac (Figura 29-43) que tem uma fem dada por ε = ε P I C O cos ⁡ w t .Mostre que a corrente no resistor é dada por I R = ε P I C O
Quando um circuito da série RLC é conectado a uma linha de 120 V rms e 60 Hz, a corrente rms no circuito é 11 A e essa corrente está à frente da tensão da linha em 45º. (a) Encontre a potência média f
Em um circuito RLC em série forçado, o gerador ideal tem uma fem de pico igual a 200 V, a resistência é 60,0 Ω e a capacitância é 8,00μ F . A indutância pode ser variada de 8,00m H para 40,0m H pela i
Uma bobina é conectada a um gerador CA de 60 Hz com uma fem de pico igual a 100 V. Nessa frequência, a bobina tem uma impedância de 10 Ω e uma reatância de 8,0 Ω. (a) Qual é a corrente de pico na bobi
Um método para medida de indutância é conectar o indutor em série com uma capacitância, uma resistência conhecida, um amperímetro ac e um gerador de sinal com frequência variável. A frequência do gera