Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 11.7 - Ex. 31
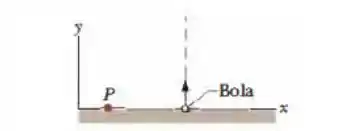
Na figura abaixo , uma bola de é lançada verticalmente para cima com uma velocidade inicial de . Qual é o momento angular da bola em relação a , um ponto a uma distância horizontal de do ponto de lançamento, quando a bola está
na altura máxima e
na metade do caminho de volta ao chão?
Qual é o torque em relação a a que a bola é submetida devido à força gravitacional quando está
na altura máxima e
na metade do caminho de volta ao chão?
Passo 1
Então galerinha bonita, quando a bola está na altura máxima, ela para momentaneamente. E sabemos que o momento angular depende da velocidade em um instante de tempo. Sendo assim, na altura máxima o momento angular é zero, afinal a velocidade é zero nesse ponto:
Passo 2
O módulo do momento angular vai ser:
Como o vetor posição é e a velocidade é , o sentido do momento angular vai ser na direção negativa de .
Show!
Agora precisamos determinar o valor da velocidade. Do movimento de queda livre, temos que a altura máxima é , relacionado pela equação de Torricelli como::
Como na altura máxima a velocidade é zero, temos:
Agora usando a mesma equação, mas para a altura de , teremos a velocidade:
Agora podemos substituir na fórmula para o momento angular, tal que:
Passo 3
O torque na altura máxima vai ser provocado pela força gravitacional . Assim:
Passo 4
Por fim o problema pede o torque a uma altura mais baixa. Bom, mas a altua não interfere na distância perpendicular em relação ao eixo de aplicação da força, então o torque permanece o mesmo.
Bora treinar mais?