Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 10.1 - Ex. 3
Uma placa metálica quadrada de lado igual a possui um eixo pivotado perpendicularmente ao plano da página passando em seu centro O (Figura 10.39). Calcule o torque resultante em torno desse eixo produzido pelas três forças mostradas na figura, sabendo que os módulos das forças são e . O plano da placa e de todas essas forças é o plano da página.
Passo 1
Oi, galerinha! Tudo bom? Bom... queremos calcular o torque resultante das forças e que estão atuando sobre uma placa metálica quadrada de lado igual a (figura abaixo):
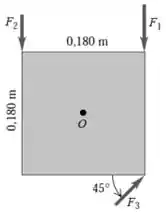
O enunciado nos diz que e .
Para resolvermos isso, temos que lembrar a definição de torque :
Onde, é a força aplicada e a distância até o ponto.
E seu módulo é:
Agora bora lá!! 😉
Passo 2
Bom... Uma ideia é desenhar um diagrama de corpo livre para entender a situação e decompor os vetores:
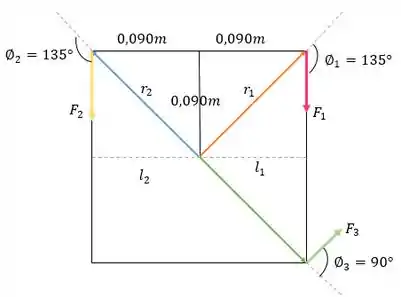
Seja no sentido anti-horário o sentido positivo de rotação.
Agora vamos aplicar essa relações para encontrar o torque de cada força!
Passo 3
Vamos começar achando o módulo de .
Repara que essa distância dada por é metade da diagonal do quadrado.
Então, usando o teorema de pitagorás temos:
Agora que achamos o e temos o ângulo vamos calcular o torque!
Passo 4
Para 1:
Com
Então,
É direcionado para o papel.
Passo 5
Para 2:
É direcionado para fora do papel.
Passo 6
Para 3:
direcionado para fora do papel.
Passo 7
E para finalizar e encontrarmos o torque total, fazemos a somatória de todos os torques que encontramos: