Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 10.2 - Ex. 8
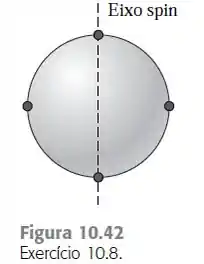
Uma casca esférica uniforme de 8,40 kg e 50,0 cm de diâmetro possui quatro pequenas massas de 2,0 kg presas à superfície externa e igualmente espaçadas entre si. Esse sistema está girando em torno de um eixo que passa pelo centro da esfera e por duas das pequenas massas (Figura 10.42). Qual torque de atrito é necessário para reduzir a velocidade escalar angular de 75,0 rpm para 50 rpm em 30,0 s?
Passo 1
Eaee, belezinha??? Bom... o enunciado nos dá a seguinte casca esférica uniforme de e de diâmetro que possui quatro pequenas massas de presas à superfície externa e igualmente espaçadas entre si:
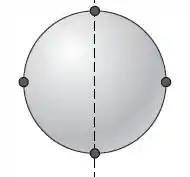
Como podemos ver na figura acima, esse sistema está girando em torno de um eixo que passa pelo centro da esfera e por duas das pequenas massas.
Queremos calcular o torque de atrito necessário para reduzir a velocidade escalar angular de para em .
Para isso, temos que saber que o torque é dado pelo produto do momento de inércia pela aceleração angular :
E que o momento de inércia para o sistema descrito é dado por:
Onde é a massa da casca esférica, é a massa das pequenas massas e é o raio da casca.
Agora bora aplicar!! 😉
Passo 2
Nós temos que:
Com: e como temos um diâmetro de , então .
E precisamos converter o raio para metros, dessa forma:
Passo 3
Temos os seguintes dados:
E vamos utilizar a equação:
Passo 4
Certo!
Agora vamos aplicar a equação do torque:
O torque é negativo porque sua direção é oposta à direção de rotação, que deve ser o caso da velocidade diminuir.