Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 10.7 - Ex. 39

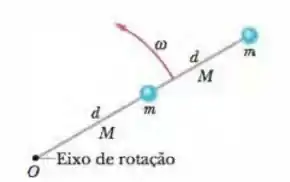
Na figura abaixo, duas partículas, ambas de massa m=0,85 Kg, estão ligadas uma à outra, e a um eixo de rotação no ponto O, por duas barras finas, ambas de comprimento d=5,6 cm e massa M=1,2 Kg. O conjunto gira em orno do eixo de rotação com velocidade angulas w=0,30 rad/s. Determine (a) o momento de inérica do conjunto em relação ao ponto O e (b) a energia cinética do conjunto.

Passo 1

Para calular o momento do inérica, que é massa multiplicada pela distância ao quadrado, precisamos lembrar de como calcular o momento de inérica de uma massa m em relação a um eixo. Para isso temos:

I = I C M + M h 2

Lembrando que h é a distância perpendicular entre o eixo e o centro de massa.

Levando em consideração a forma geométrica da barra, vamos obter:

I b a r r a = 1 12 M L 2

Como são duas barras e duas massas, para calcular então o momento de inérica, logo:

I = I 1 + I 2 + I 3 + I 4

Passo 2

Para I 1 , que seria o momento de inércia da primeira barra, temos:

I 1 = 1 12 M d 2 + M 1 2 d 2

Já para I 2 , que seria o momento de inércia da primeira massa, temos:

I 2 = m d 2

Agora para I 3 , que seria o momento de inércia da segunda barra, e a distância do eixo de rotação aumenta, vamos ter que

I 3 = 1 12 M d 2 + M 3 2 d 2

E para I 4 , que seria o momento de inércia da segunda massa, e está localizada na extremidade da barra, obtemos:

I 4 = m ( 2 d ) 2

Passo 3

Juntando tudo e substituindo os valores apresentados no problema para as barras, ficamos assim:

I b a r r a s = I 1 + I 3

I b a r r a s = 1 12 M d 2 + M 1 2 d 2 + 1 12 M d 2 + M 3 2 d 2

I b a r r a s = 8 3 M d 2

Logo:

I b a r r a s = 8 3 1,2 0,056 2

I b a r r a s = 0,0100352

Juntando tudo e substituindo os valores apresentados no problema para as massas, teremos que:

I m a s s a s = I 2 + I 4

I m a s s a s = m d 2 + m 2 d 2

I m a s s a s = 5 m d 2

Tal que:

I m a s s a s = 5 ( 0,85 ) 0,056 2

I m a s s a s = 0,013328

Isso quer dizer que o momento de inércia total é dado comoa soma dessaes dois momentos separados, de forma que:

I = I b a r r a s   + I m a s s a s

I = 0,0100352 + 0,013328

I = 0,023   kg. m 2

Passo 4

Para a energia cinética, neste caso, fica assim:

K = 1 2 I ω 2

Como já foi encontrado o valor do momento de inércia no ítem (a), é só a gente substituir ele na fórmula, tal que:

K = 1 2 ( 0,02336 ) 0,30 2

K = 1,1 × 10 - 3   j

K = 11   mJ

Resposta

  1. I = 0,023   kg. m 2
  2. K = 11   mJ
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Você deseja localizar o centro de gravidade de um objeto achatado e de formato arbitrário. Você pendura o objeto de um ponto e um fio de prumo do mesmo ponto. Então, você traça uma linha vertical no o
Use o teorema dos eixos paralelos e o resultado do problema 41 para encontrar o momento de inércia do sistema de quatro partículas da figura 9-45 em relação a um eixo que passa pelo centro de massa e
Um cilindro oco tem massa m , raio externo R 2 e raio interno R 1 . Use integração para mostrar que o momento de inércia em relação a seu eixo é dado por I = 1 2 m ( R 2 2 + R 1 2 ) . Dica: reveja a s
Um disco uniforme de raio r e massa M gira em torno de um eixo horizontal paralelo ao seu eixo de simetria e que passa por um ponto de seu perímetro, de forma a poder oscilar livremente em um plano ve
Você pendura um aro fino de raio R em um prego na periferia do aro. Você o desloca lateralmente (dentro do plano do aro) até um ângulo β a partir de sua posição de equilíbrio e a seguir o liberta. Qua