Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 14.6 - Ex. 50
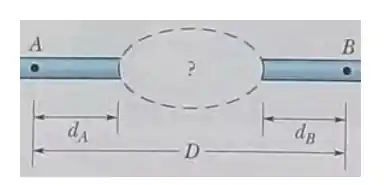
A figura abaixo mostra dois segmentos de uma antiga tubulação que atravessa uma colina; as distâncias são . O raio do cano do lado de fora da colina é ; o raio do cano no interior da colina, porém, não é mais conhecido. Para determiná-lo, o s engenheiros hidráulicos verificaram inicialmente que a velocidade da água nos segmentos à esquerda e à direita da colina era de . Em seguida, os engenheiros introduziram um corante na água no ponto A e observaram que levava para chegar ao ponto . Qual é o raio médio do cano no interior da colina?
Passo 1
Belezera galerinha, primeiramente precisamos notar que as seções do lado esquerdo e direito possuem um comprimento total de Tal comprimento é percorrido com uma velocidade de . Isso ocorre em um intervalo de tempo igual a Então, de acordo com o enunciado, é necessário um tempo:
A partir disso, podemos inferir que a velocidade na seção média é dada por:
Logo:
Passo 2
Da equação da continuidade, temos:
Isolando , chegamos em:
