Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 14.6 - Ex. 49
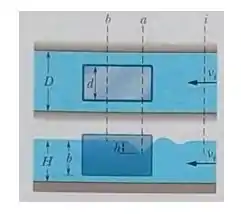
A figura mostra um canal onde se encontra uma barcaça ancorada com de largura e de calado. O canal tem uma largura , e uma profundidade e nele circula água com uma velocidade . Suponha que a vazão em torno da barcaça é uniforme. Quando a água passa pela proa da barcaça sofre uma queda brusca de nível conhecida como efeito canal. Se a queda é de , qual é a velocidade da água ao passar ao lado da barcaça (a) pelo plano vertical indicada pela retatracejada a e (b) pelo plano vertical indicado pela reta tracejada b? A erosão causada pelo aumento da velocidade é um problema que preocupa os engenheiros hidráulicos.
Passo 1
Letra a):
Primeiramente, vamos lembrar da equação da continuidade:
Aplicada entre dois pontos e . Considerando os pontos localizados antes do encontro da água com a barcaça e após, temos:
Assim, da equação da continuidade, temos:
Passo 2
Substituindo os valores do enunciado na expressão acima, obtemos que:
Passo 3
Letra b):
No ponto b, a área da seção transversal é dada por . Portanto, pela equação da continuidade, temos:
Passo 4
Substituindo os valores do enunciado na expressão acima, chegamos em:
