Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 6.1 - Ex. 68
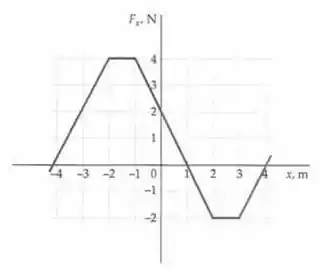
A figura abaixo mostra a força que atua sobre urna partícula de 0,500 kg. (a) Do gráfico, calcule o trabalho realizado pela força enquanto a partícula se move de até os seguintes valores de x: -4,00, -3,00, -2,00, -1,00, +1,00, +2,00, +3,00, e +4,00. (b) Se a partícula parte com uma velocidade de 2,00 m/s no sentido +x, até onde ela viajará ao longo deste eixo até parar?
Passo 1
Letra (a)
O trabalho é igual à área embaixo do gráfico versus posição . Que é o nosso caso! Então a gente precisa achar a área abaixo do nosso gráfico entre e cada ponto que ele pede.
Para achar a área, não vamos integrar, porque não temos função para integrar. Vamos dividir a área abaixo do gráfico em formas mais simples de calcular a área. Podemos usar triângulos e retângulos.
Para . Percebe que a força nesse intervalo tem valores positivos mas o deslocalmento foi negativo (saiu de 0 para ). Ou seja, a força está no sentido oposto do deslocamento, por isso temos trabalho negativo.
Calculando a área abaixo do gráfico no intervalo , vemos que temos 3 triângulos de altura 2 e base 1, e temos 4 retângulos de altura 2 e base 1. A área fica:
Assim o trabalho fica:
Passo 2
Vamos fazer o mesmo para . Aqui temos trabalho negativo também porque o deslocamento é negativo e a força é positiva.
Calculando a área abaixo do gráfico no intervalo , vemos que temos 2 triângulos de altura 2 e base 1, e temos 4 retângulos de altura 2 e base 1. A área fica:
Assim o trabalho fica:
De forma análoga, para o trabalho é negativo. Calculando a área de forma semelhante achamos , assim:
E para também temos trabalho negativo que vale:
Passo 3
Agora para , trabalho vai ser positivo porque o deslocamento nesse caso é positivo e a força também.
A área é um triângulo:
Assim:
Mas agora repara que para , e vamos ter uma situação diferente porque a força muda de sinal durante o deslocamento. Aí o que a gente faz? Como o deslocamento é positivo, o trabalho vai ter sinal igual ao da força.
Então o que a gente pode fazer é dar sinal positivo para a área acima do eixo horizontal onde e sinal negativo para . Somando achamos o trabalho com o sinal certinho dele.
Para , temos no intervalo um triângulo acima do eixo horizontal e um triângulo abaixo do eixo. Então o trabalho fica:
Pesando parecido para :
E para :
Colocando tudo que a gente achou numa tabelinha:
Passo 4
Letra (b)
Então a gente quer saber o quanto a partícula viaja até parar, ou seja, até termos .
Se a rapidez dela é zero no repouso, a energia cinética também. Então podemos dizer que queremos saber onde sua energiua cinética zera depois que ela sai da origem indo no sentido positivo, já que sua velocidade na origem é positiva.
Cara, falou de trabalho e rapidez no mesmo contexto, cê pensa logo no teorema do trabalho-energia cinética. Olha a expressão dele:
Isso diz que o trabalho total feito em uma partícula é igual à variação de energia cinética. No nosso caso, a energia cinética final é nula, então:
Passo 5
No ponto inicial, em , a energia cinética é:
Ele dá a velocidade e a massa da partícula nesse ponto, então podemos substituir:
O teorema fica:
Passo 6
Agora a gente precisa ver até que ponto no sentido positivo temos o trabalho total de .
Percebe que no intervalo temos um trabalho total de . Já no intervalo a área abaixo do gráfico nos dá um trabalho de . Como temos uma variação linear da força, na metade de , em , vamos ter .
Aí repara que se dá e que dá , o trabalho total no intervalo vai ser
Que é o trabalho que indica que a partícula parou!
Então ela para em .
Resposta
Letra (a):
Letra (b):