Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 10.1 - Ex. 45
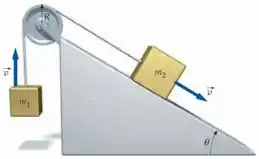
Na figura, o plano inclinado é sem atrito e o fio passa pelo centro de massa de cada bloco. A polia tem um momento de inércia e raio . (a) Determine o torque resultante sobre o sistema (as duas massas, o fio e a polia) em relação ao centro da polia. (b) Escreva uma expressão para a quantidade de movimento angular total do sistema em relação ao centro da polia. Suponha as massas se deslocando com uma rapidez . (c) Determine a aceleração das massas usando seus resultados das partes (a) e (b) e igualando o torque resultante à taxa de variação da quantidade de movimento angular do sistema.
Passo 1
(a) Vamos procurar uma expressão para o torque resultante em relação ao centro da polia. Vamos considerar o sentido positivo como aquele que favorece a rotação da polia no sentido horário.
Em todos os casos, a distância entre o ponto onde a força é aplicada sobre a polia e o centro é o raio .
As forças que produzem torque sobre a polia são os pesos dos dois blocos:
Passo 2
(b) Para escrever o momento angular total do sistema em relação ao centro da polia, vamos primeiro considerar o momento da própria polia:
Onde , então:
E os momentos angulares das duas massas podem ser escritos da seguinte forma:
Já que é a distância entre o centro da polia e as direções das velocidades de ambas as massas.
Então o momento angular total é:
Passo 3
(c) Agora que temos o momento angular resultante , podemos tirar sua derivada temporal para encontrar o torque resultante:
E a única variável que depende do tempo nessa expressão é , as demais são constantes. Como a derivada temporal da rapidez é a aceleração:
E usando a expressão que deduzimos para o torque no item (a) podemos encontrar uma fórmula para a aceleração do sistema:
Isolando :
Resposta
(a) .
(b) .
(c) .