Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 10.1 - Ex. 14
Você está andando em direção ao norte, e na sua mão esquerda você está carregando uma mala que contém uma roda massiva girante, montada sobre um eixo preso às partes anterior e posterior da maleta. A velocidade angular do giroscópio aponta para o norte. Agora, você começa a se virar para caminhar para o leste. Em consequência, a parte anterior da maleta (a) resistirá à sua tentativa de virá-la e tentará manter sua orientação original, (b) resistirá à sua tentaiva de virá-la e puxará para o oeste, (c) irá levantar-se, (d) irá inclinar-se para baixo, (e) não apresentará nenhum efeito.
Passo 1
Vamos lembrar da seguinte relação:
Ou seja, o vetor do torque é paralelo à variação do vetor momento angular. No instante e, que você começa a girar para mudar de norte para leste, o vetor aponta para o leste.
Passo 2
Portanto, também aponta para o leste, então em que direção aponta a força que produz um torque como esse?
Onde é um vetor posição que sai do centro de roda e vai até o ponto de aplicação da força . O desenho a seguir é uma visão de cima da cabeça da pessoa que carrega a maleta:
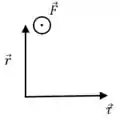
O mesmo resultado seria obtido se invertêssemos os sinais de e , mas é mais coerente pensar que a força exercida pela pessoa sobre a maleta é para cima.
Passo 3
Então até aqui sabemos que você precisa exercer uma força apontando para cima sobre a maleta, consequentemente, a maleta irá exercer uma força de mesmo módulo apontando para baixo sobre você.
E portanto a maleta irá inclinar-se para baixo.
Resposta
Letra (d).