Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 10.1 - Ex. 40

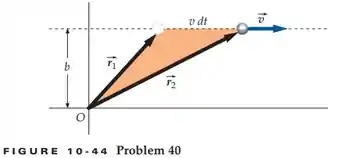
Uma partícula, de massa m , viaja com uma velocidade constante v → ao longo de uma linha reta que dista b da origem O (figura 10-44). Seja d A a área varrida pelo vetor posição da partícula, em relação a O , durante o intervalo de tempo d t . Mostre que d A / d t é constante e igual a L / 2 m , onde L é a magnitude da quantidade de movimento angular da partícula em relação à origem.

Passo 1

Repara que essa variação de área que ele diz no enunciado é a área do triângulo maior menos a do triângulo menor, viu?! Vamos fazer o seguinte, considere x a componente horizontal de r 1 e x + Δ x a de r 2 . Então vai ficar assim:

Δ A = A g r a n d e - A p e q u e n a

A g r a n d e = 1 2 ⋅ b ⋅ x + Δ x

E,

A p e q u e n a = 1 2 ⋅ b ⋅ x

Passo 2

Δ A = 1 2 ⋅ b ⋅ x + Δ x - 1 2 ⋅ b ⋅ x

Logo,

Δ A = 1 2 ⋅ b ⋅ Δ x

quando temos intervalos muito pequenos de tempo ( Δ t → 0 ) :

d A d t = 1 2 ⋅ b ⋅ d x d t = 1 2 ⋅ b ⋅ v

Passo 3

Pra finalizar, vamos relacionar isso com o momento angular! Sabemos o seguinte:

L = m v | r 1 → | s e n ( θ )

d A d t = 1 2 b v

Da figura, podemos ver que r 1 → s e n θ = b !

L = m v b → b = L m v

Voltando na nossa relação:

d A d t = b v 2 = l 2 m v ⋅ v = L 2 m  

Demonstrado como o enunciado pediu :D

Resposta

Demonstração

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Considere um sistema isolado de duas partículas de massas m 1 e m 2 . Exprima o vetor momento angular total do sistema relativo ao seu CM em função da massa reduzida μ , do vetor posição r de m 2 em r
Uma bolinha presa a um fio de massa desprezível gira em torno de um eixo vertical com velocidade escalar constante, mantendo-se a uma distância d = 0.5 m do eixo; o ângulo θ é igual a 30 ° . O fio pas
Seja C uma curva plana fechada orientada. A área orientada S associada a C é definida como um vetor perpendicular ao plano de C, de magnitude igual à área S contida dentro de C e sentido tal que, vist
Vamos calcular a posição y da carga caindo anexada ao guincho no Exemplo 9-8 como uma função do tempo por integração numérica. Deixe a direção + y ser reta para baixo. Então, v y = d y / d t , ou t =
Qual é a velocidade angular de um caro que faz uma curva circular com 110m de raio a 50k m / h ?