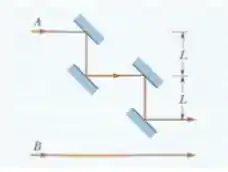
Na figura abaixo temos as ondas sonoras e , de mesmo comprimento de onda , estão inicialmente em fase e se propagam para a direita, como indicam os dois raios. A onda é refletida por quatro superfícies, mas volta a se propagar na direção e no sentido original. Que múltiplo do comprimento de onda é o menor valor da distância na figura para o qual e estão em oposição de fase após as reflexões?

Agora a diferença de percurso é dada por:

Pelo desenho podemos ver que a onda percorre uma distância maior. Ela percorre o mesmo percurso de na parte horizontal, digamos , mais a parte vertical que é . Assim os caminhos percorridos para e são:

Assim a diferença de caminho é dada por:

Vamos substituir na relação para interferência destrituva:

Como o problema pede o menor valor da distância , temos isso fazendo :

Assim temos:

Ou seja, o menor múltiplo de vai ser .