Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 12.Problemas Adicionais - Ex. 55
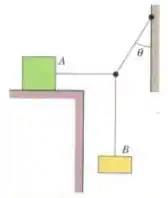
Na Figura, o bloco A, com uma massa de , está em repouso, mas escorregaria se o bloco , que tem uma massa de , fosse mais pesado. Se , qual é o coeficiente de atrito estático entre o bloco e a superfície na qual está apoiado?
Passo 1
A questão mostra um sistema em equilíbrio, e diz que um aumento na massa do bloco seria suficiente pra acabar com isso. Isso quer dizer que a massa do bloco já é a maior massa que permite o equilíbrio!
Vamos então aplicar as equações de equilíbrio em todos os corpos. No caso, não faz sentido usar o equilíbrio dos torques porque o sistema não envolve rotações.
Passo 2
Começando pelo bloco :
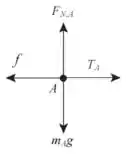
Onde é a força de atrito entre o bloco e a superfície, é a tração da corda que puxa o bloco , é a força normal que a superfície faz sobre o bloco, e é a força peso.
Como o bloco não se mexe, temos:
Pronto.
Passo 3
Agora vamos falar do bloco :
Como esse bloco também não se mexe, vamos ter o seguinte:
Lembrando que esse , pelo enunciado, já é a massa máxima que o sistema aguenta.
Passo 4
Por fim, vamos analisar aquele ponto que une todas as cordas:
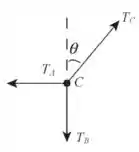
Aqui vamos ter duas equações, pois vamos exigir o equilíbrio tanto na vertical quanto na horizontal:
Agora vamos juntar todas as informações.
Passo 5
No final ficamos com as seguintes equações:
(1)
(2)
(3)
(4)
(5)
Nosso objetivo é encontrar o coeficiente de atrito entre o bloco e a superfície. A fórmula envolvendo essa grandeza é:
Mas na equação (4) já tínhamos achado que , então:
Agora vamos começar a mexer nesse sistema de equações:
Dividindo a equação (1) pela (2):
E agora usando as equações (3) e (5) pra substituir as tensões:
Agora já podemos isolar o coeficiente de atrito:
E substituir os valores:
Pronto!
Resposta
O coeficiente de atrito é .