Exercícios de MHS + Colisões - Lista de Exercícios Resolvida

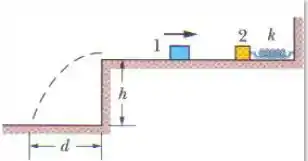
A figura abaixo mostra o bloco 1, de massa , deslizando para a direta, sobre uma superfície elevada, com uma velocidade de s. O bloco sofre uma colisão elástica com o bloco 2, inicialmente em repouso, que está preso a uma mola de constante elástica (Suponha que a mola não afete a colisão.) Após a colisão, o bloco 2 inicia um MHS com um período de e o bloco 1 desliza para fora da extremidade oposta da superfície elevada, indo cair a uma distância horizontal de dessa superfície, depois de descer uma distância de . Qual é o valor de ?

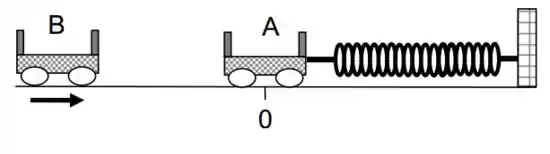
Um carrinho de massa , inicialmente em repouso no ponto , está preso a uma mola relaxada de constante elástica e pode se deslocar sem atrito sobre uma mesa horizontal. Um carrinho de massa se aproxima com uma velocidade e colide frontalmente com o carrinho . Após a colisão, que é completamente inelástica, os carrinhos passam a oscilar juntos. Encontre, em função dos dados acima,

1. A velocidade dos blocos logo após a colisão.
2. A frequência angular de oscilação e a amplitude, , do movimento.
3. Considerando o instante de choque, obtenha a constante de fase e escreva a posição em função do tempo,
4. Suponha que ao atingir a posição o carrinho se solte do sistema. Encontre a nova velocidade do carrinho ao passar pelo ponto

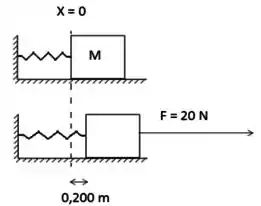
Um bloco de é unido a uma mola e colocado em uma superfície horizontal sem atrito. Uma força horizontal de é necessária para manter o bloco em repouso quando é puxado de de sua posição de equilíbrio. O bloco é liberado do repouso a partir deste ponto e realiza um movimento harmônico simples.

1. Encontre a constante de força da mola e a frequência de oscilação.
2. Determine a energia cinética máxima do bloco.
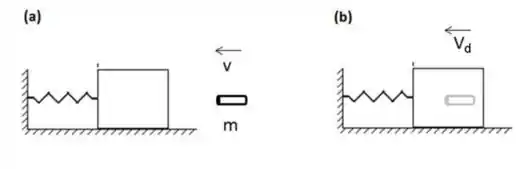
3. Considere agora que o bloco esteja em repouso na sua posição de equilíbrio e um projétil de massa com velocidade de atinge o bloco, como mostra a figura (a) abaixo. O projétil fica preso no bloco, como mostrado na figura (b), e o sistema bloco+projétil passa a oscilar num movimento harmônico simples. Determine a amplitude do MHS resultante.



4. Se o projétil do item c) atingir o bloco quando este se encontra com velocidade nula na posição , qual será a nova amplitude do movimento?

Imagine um experimento em que temos um carrinho de massa , inicialmente em repouso, preso a uma mola relaxada de constante elástica e que pode se deslocar sem atrito sobre uma mesa horizontal. Nesse experimento, um carrinho de massa se aproxima com uma velocidade e colide frontalmente com o primeiro carrinho. Após a colisão, que é completamente inelástica, os carrinhos passam a oscilar juntos.

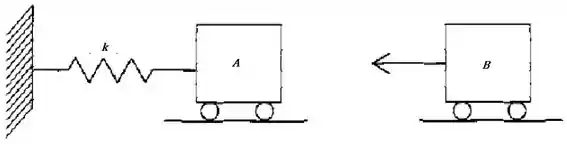
Calcule a velocidade dos blocos logo após a colisão, a frequência angular de oscilação e a amplitude, , do movimento.

Um bloco de massa , em repouso numa mesa horizontal sem atrito, é ligado a um suporte rígido por duas molas de constante elástica e , de modo que . Uma bala bala Juquinha, de preferência... pra quê falar de mais violência ) de massa e velocidade atinge o bloco como mostrado na figura abaixo (e fica grudada nele).

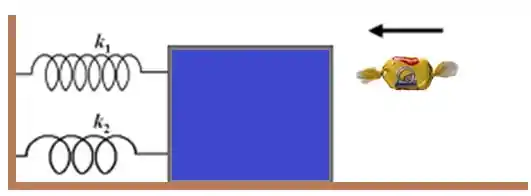
De posse dessas informações, determine a velocidade do conjunto imediatamente após a colisão e a amplitude do movimento harmônico simples associado.

(Obs.: Dica do Dexter – Confira o nosso material de associação de molas)

Um bloco de massa , em repouso numa mesa horizontal sem atrito, é ligado a um suporte rígido por duas molas de constante elástica e . Uma bala de massa e velocidade atinge o bloco como mostrado na figura abaixo.

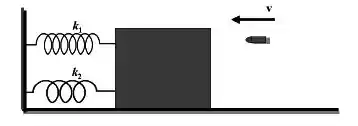
Este sistema de duas molas da figura acima é equivalente a um sistema composto por apenas uma mola cuja constante elástica vale:

1. Deduza a expressão .

Considere e determine em função de , , e :

2. A velocidade do bloco imediatamente após a colisão.
3. A amplitude do movimento harmônico simples.

Um corpo de massa colide com uma plataforma de massa , inicialmente em repouso e presa a uma mola de constante e massa desprezível (a outra extremidade da mola mantém-se presa a uma parede). No momento da colisão, a mola está relaxada e a velocidade do corpo é . O sistema está imerso em um fluido com constante de amortecimento .

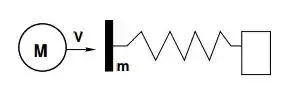
Se a colisão entre o corpo e a plataforma for completamente inelástica, determine:

1. A frequência natural de oscilação do sistema na ausência de amortecimento.
2. O regime de oscilação amortecida.
3. A velocidade do corpo no instante logo após a colisão.
4. A posição do corpo em função do tempo (considere a posição de equilíbrio e o instante logo após a colisão).

Um carrinho (1) de massa M = 0,250 kg está preso à extremidade de uma mola realizando movimento harmônico simples com intervalos de tempo de 0,1 s entre dois extremos consecutivos de sua oscilação. No instante inicial, ele se move em direção à parede, passando pela posição x = 0 com velocidade v = 20 m/s 62,8 m/s.

Considere que o carrinho (1) esteja em repouso na posição de equilíbrio quando sofre uma colisão perfeitamente inelástica com o carrinho (2), de massa igual a 1,750 kg, quando o mesmo apresentava uma velocidade de 16 m/s 50,3 m/s em direção à parede.

a) Determine a velocidade dos carrinhos imediatamente após a colisão.

b) Determine a nova frequência angular e o novo período do MHS dos carrinhos acoplados.

c) Determine a nova amplitude do MHS e a nova energia total do sistema.

Considere dois pêndulos simples, de mesmo comprimento l, presos a um mesmo ponto como mostra a figura. A partícula de massa é solta do repouso a uma altura z em relação à posição de equilíbrio e atinge a partícula de massa em t = 0 s. Anteriormente, a partícula de massa estava em repouso, na posição de equilíbrio. Após a colisão as duas partículas permanecem juntas.

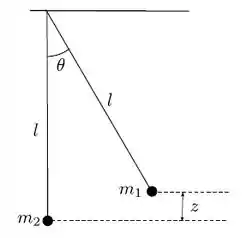
Considerando que a aceleração da gravidade g é conhecida e que, tanto antes quanto depois da colisão, vale a aproximação de pequenos ângulos para ambos os pêndulos, a amplitude do movimento pode ser escrita como:

(a)

(b)

(c)

(d)

(e)

Um bloco de é unido a uma mola e colocado em um superfície horizontal sem atrito. Uma força horizontal de é necessária para manter o bloco em repouso quando é puxado de de sua posição de equilíbrio. O bloco é liberado do repouso a partir deste ponto e realiza um movimento harmônico simples.

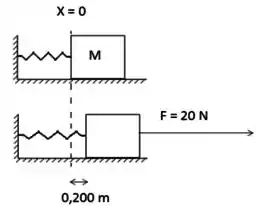
1. Encontre a constante de força da mola e a frequência de oscilação.
2. Determine a energia cinética máxima do bloco.
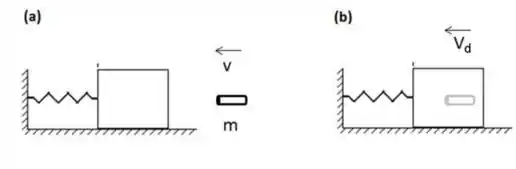
3. Considere agora que o bloco esteja em repouso na sua posição de equilíbrio e um projétil de massa com velocidade de atinge o bloco, como mostra a figura (a) abaixo. O projétil fica preso no bloco, como mostrado na figura (b), e o sistema bloco+projétil passa a oscilar num movimento harmônico simples . Determine a amplitude do MHS resultante.



4. Se o projétil do item c) atingir o bloco quando este se encontra com velocidade nula na posição , qual será a nova amplitude do movimento?

Um carrinho de massa , inicialmente em repouso no ponto , está preso a uma mola relaxada de constante elástica e pode se deslocar sem atrito sobre uma mesa horizontal. Um carrinho de massa se aproxima com uma velocidade e colide frontalmente com o carrinho . Após a colisão, que é completamente inelástica, os carrinhos passam a oscilar juntos. Encontre, em função dos dados acima,

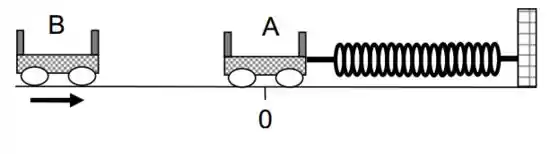
1. A velocidade dos blocos logo após a colisão.
2. A frequência angular de oscilação e a amplitude, , do movimento.
3. Considerando o instante de choque, obtenha a constante de fase e escreva a posição em função do tempo,
4. Suponha que ao atingir a posição o carrinho se solte do sistema. Encontre a nova velocidade do carrinho ao passar pelo ponto

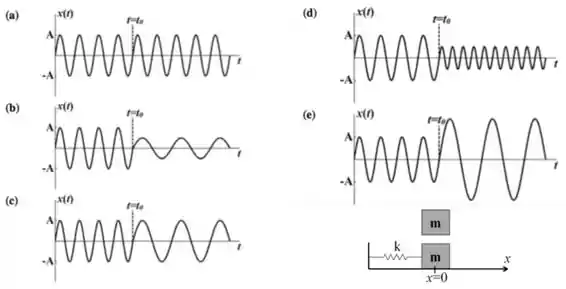
Um oscilador harmônico simples constituído por um bloco de massa m e uma mola de constante elástica realiza um movimento periódico com amplitude em torno da posição de equilíbrio . No instante , o bloco passa pela posição , e no mesmo instante, um outro bloco, de massa m, é solto sobre o primeiro bloco e a nele se fixa. Qual é o gráfico que melhor representa a posição do primeiro bloco em função do tempo?