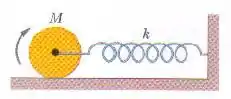
Na figura um cilindro maciço preso a uma mola horizontal () rola sem deslizar em uma superfície horizontal. Se o sistema é liberado a partir do repouso quando a mola está distendida de , determine (a) a energia cinética de translação e (b) a energia cinética de rotação do cilindro ao passar pela posição de equilíbrio. (c) Mostre que, nessas condições, o centro de massa do cilindro executa um movimento harmônico simples de período

onde é a massa do cilindro. (Sugestão: calcule a derivada da energia mecânica total em relação ao tempo.)

Falaaa galerinha bonita, tudo beleza?

Saca só, nesse exercício aqui o enunciado nos diz que um cilindro maciço preso a uma mola horizontal de constante elástica rola sem deslizar sobre uma superfície horizontal. Sabendo que o sistema é liberado a partir do repouso quando a mola estaá distendida de , o enunciado pede pra gente determinar na letra (a), a energia cinética de translação.

Mas calma lá meu patrão, vamos devagarinho. O problema aqui é que além de ir pra trás e pra frente com a mola, o cilindro vai rolar, ou seja, precisamos considerar a energia cinética associada a essa rotação também.

Nosso primeiro objetivo é achar a energia cinética de translação quando o cilindro passa pelo ponto de equilíbrio. Vamos usar a lei de conservação de energia:

A gente sabe que quando o cilindro passa pelo ponto de equilíbrio, teremos que:

Onde é a energia potencial da mola, enquanto que é a energia cinética total dada pela soma da energia cinética de rotação com a energia cinética de translação, sendo assim:

Sendo o momento de inércia do cilindro em relação ao centro de massa, a velocidade de translação, a frequência angular e a amplitude do MHS. Como , teremos que:

Logo:

MAASSSSS, agora que vem a malandragem.

Porque queremos encontrar a energia cinética de rotação , só que temos apenas um termo dado como , então podemos com toda sagacidade do mundo, multiplicar os dois lados da equação por , de modo que:

Onde é exatamente nossa energia cinética de rotação , tal que:

Como o enunciado nos deu que e , vamos obter que: