Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 8.5 - Ex. 122

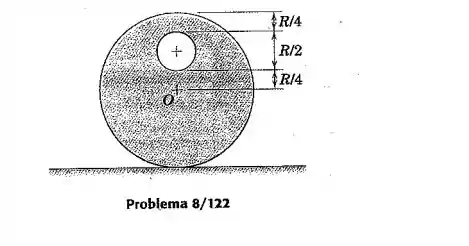
Um furo de raio R / 4 é perfurado através de um cilindro de raio R para formar um corpo de massa m como mostrado. Se o corpo rola sobre a superfície horizontal sem deslizar, determine o período τ para pequenas oscilações.

Passo 1

Para esse problema vamos usar as relações da posição do centro de massa relacionando com a área da superfície e conservação de energia mecânica para encontrarmos a frequência de oscilação. Usaremos também o teorema dos eixos paralelos para encontrar o momento de inércia no centro de massa e as relações de velocidade relativa para um referencial não-inercial.

Passo 2

Nesse problema, temos que uma parte da área foi retirada e como não temos mais uma simetria em torno da origem seria melhor mudarmos e olhar em torno do centro de massa. Para isso, precisamos encontrar a posição do centro de massa. Podemos calcular, para esse caso, a posição do centro de massa em relação a área do objeto. Assim, nossa equação ficará

Y c m = ∑ y ' ⋅ A ' ∑ A

Onde A ' é a área da parte que está faltando e y ' é a distância até a origem a partir do centro de massa da área faltante e ∑ A é a área total do sistema menos a área do buraco. Substituindo os valores na equação, ficamos com

Y c m = ∑ y ' ⋅ A ' ∑ A = - R 2 ⋅ π ⋅ R 2 16 π ⋅ R 2 - π ⋅ R 2 16 = - R 30

Agora precisamos encontrar o momento de inércia do sistema. Ele será dado pelo momento de inércia do sistema completo menos o do buraco. Assim, temos que

I o = I d i s c o - I b u r a c o = 1 2 ⋅ m 1 ⋅ R 2 - 1 2 ⋅ m 2 ⋅ R 2 16 + m 2 ⋅ R 2 4 = 1 2 ⋅ R 2 ⋅ m 1 - 9 16 ⋅ m 2

Mas temos que podemos escrever m 1 e m 2 em termos da densidade do disco. Temos que

ρ = m 1 A 1 = m 1 π ⋅ R 2

E

ρ = m 2 A 2 = m 2 π ⋅ R 2 16

Substituindo, chegamos que

I O = 247 512 ⋅ R 4 ⋅ ρ ⋅ π

Mas temos também que a densidade também pode ser escrita como

ρ = M A = M π ⋅ R 2 - π ⋅ R 2 16

Substituindo novamente, chegamos que

I O = 247 480 ⋅ M ⋅ R 2

Achamos o momento de inércia para o disco girando em torno da origem, mas queremos o momento de inércia em torno do centro de massa, então usando o teorema dos eixos paralelos, temos que

I c m = I O - M ⋅ Y c m 2 = 247 480 ⋅ M ⋅ R 2 - M ⋅ R 2 900 = 0.5135   M ⋅ R 2

Como o centro de massa está acelerando em relação a origem, precisamos usar a relação de velocidade relativa para um referencial não inercial. Temos então que

V → G = V → o + ω → × r → G O = - R ⋅ ω ⋅ i → + ω ⋅ k → × R 30 ⋅ sin ⁡ θ ⋅ i → - cos ⁡ θ ⋅ j →

V G = ω ⋅ R 30 ⋅ cos ⁡ θ - R ⋅ i → + R 30 ⋅ sin ⁡ θ ⋅ j →

V G 2 = ω 2 1.001 ⋅ R 2 - 1 15 ⋅ R 2 ⋅ cos ⁡ θ

Aplicando agora a conservação de energia, temos que E = U + T . Com

U = m ⋅ g ⋅ Y c m ⋅ 1 - cos ⁡ θ

T = 1 2 ⋅ I G ⋅ θ ˙ 2 + 1 2 ⋅ M ⋅ V G 2

Substituindo na energia, temos que

E = 1 2 ⋅ 0.5135   M ⋅ R 2 ⋅ θ ˙ 2 + 1 2 ⋅ M ⋅ θ ˙ 2 1.001 ⋅ R 2 - 1 15 ⋅ R 2 ⋅ cos ⁡ θ + M ⋅ g ⋅ R 30 ⋅ 1 - cos ⁡ θ

Como temos que a energia é constante, se derivarmos em relação ao tempo, temos que d E d t = 0 . Assim, chegamos que

0 = 0.5135 ⋅ θ ˙ ⋅ R 2 ⋅ θ ¨ + θ ˙ ⋅ θ ¨ ⋅ 1.001 ⋅ R 2 - 1 15 ⋅ R 2 ⋅ cos ⁡ θ + 1 2 ⋅ θ ˙ 2 ⋅ 1 15 ⋅ R 2 ⋅ sin ⁡ θ ⋅ θ ˙ + g ⋅ R 30 ⋅ sin ⁡ θ ⋅ θ ˙

0.5135 ⋅ R 2 ⋅ θ ¨ + θ ¨ ⋅ 1.001 ⋅ R 2 - 1 15 ⋅ R 2 ⋅ cos ⁡ θ + 1 2 ⋅ θ ˙ 2 ⋅ 1 15 ⋅ R 2 ⋅ sin ⁡ θ + g ⋅ R 30 ⋅ sin ⁡ θ = 0

Se assumirmos agora θ pequeno, temos que θ ˙ → 0 , cos ⁡ θ → 1 , sin ⁡ θ → θ . Substituindo na equação então, chegamos que

1.448 ⋅ R 2 ⋅ θ ¨ + 0.0333 ⋅ g ⋅ R ⋅ θ = 0

θ ¨ + 0.0230 ⋅ g R ⋅ θ = 0

ω n = 0.0230 ⋅ g R = 0.152 ⋅ g R

τ = 2 ⋅ π ω n = 41.3 ⋅ R g

Resposta

τ = 41.3 ⋅ R g

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O eixo de rotação da plataforma giratória está inclinado em um ângulo α a partir da vertical. A haste da plataforma é livremente articulada nos mancais que não são mostrados. Se um pequeno bloco de ma
Desenvolva a expressão para a frequência natural f n do sistema composto de dois cilindros circulares homogêneos, cada um de massa M, e o elemento de ligação AB de massa m. Assuma pequenas oscilações.
A haste esbelta uniforme de comprimento l e massa m 2 está fixada ao disco uniforme de raio l / 5 e massa m 1 . Se o sistema é apresentado em sua posição de equilíbrio, determine a frequência natural
As extremidades da barra uniforme de massa m deslizam livremente nas ranhuras vertical e horizontal, como mostrado. Se a barra está em equilíbrio estático quando θ = 0 , determine a frequência natural
A suspensão dianteira de um automóvel é apresentada. Cada uma das molas helicoidais possui uma rigidez de 46.8 kN/m. Se a massa da extremidade dianteira do chassi e da parte equivalente da carroceria,