118. Cada um dos dois blocos deslizantes possui uma massa e está limitado a se deslocar em uma das ranhuras radiais lisas do volante, que é acionado a uma velocidade angular constante . Cada uma das quatro molas possui uma rigidez É correto afirmar que o sistema composto pelo volante, blocos e molas possui uma energia constante? Explique sua resposta.
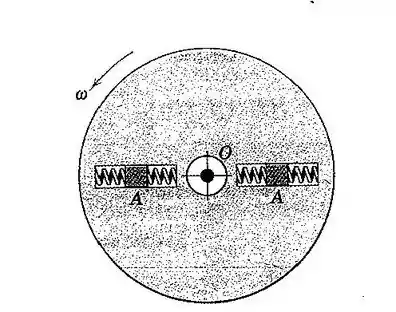
Passo 1
Bom, primeiro vamos lembrar do que é composta a energia total de um sistema:
Onde é a energia potencial e é a energia cinética.
Para um sistema isolado:
Mas nesse caso, como temos constante, não teremos uma energia total constante. Mas por que?
Bom, temos que lembrar que é um corpo rígido e com isso, sua rotação também tem uma energia associada. Como se trata de um círculo, a energia de rotação fica:
Onde é a frequência angular e é o momento de inércia.
Como é constante neste exercício, a energia de rotação só será alterada quando alterarmos o momento de inércia do volante. Isso ocorre quando os blocos dentro do volante deslizam para mais dentro do volante ou para mais fora. Como essa energia de rotação é equivalente à energia cinética do volante, então quanto maior o , maior a energia cinética do sistema.
E quando teremos um maior? Quando os blocos estiverem para os lados mais próximos da borda, pois lembrando a fórmula de momento de inércia de um disco:
Podemos ver, então, que há um aumento de quando os blocos estão mais distantes do centro.
Portanto, para uma mesma energia potencial, a energia cinética do sistema será diferente para os casos citados, e consequentemente a energia não será constante.
Resposta
A energia não será constante.