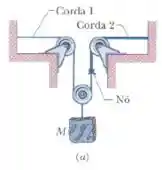
Na figura , a corda tem uma massa específica linear de e a corda tem uma massa específica linear de . As cordas estão submetidas à tensão produzida por um bloco suspenso de massa . Calcule a velocidade da onda (a) na corda e (b) na corda . (Sugestão: quando uma corda envolve metade de uma polia, exerce sobre a polia uma força duas vezes maior que a tensão da corda). Em seguida, o bloco é dividido em dois blocos (com e o sistema é montado como na figura . Determine (c) e (d) para que as velocidades das ondas nas duas cordas sejam iguais.

Na situação da figura (a), qual é a força que puxa as cordas? Exatamente, é só o peso daquela massa .

Primeiro vamos calcular o peso do bloco:

Então o bloco “passa” essa tensão para aquela corda que está presa diretamente nele, certo? Mas ainda tem mais um detalhe, aquela sugestão do enunciado disse que a força sobre a polia é o dobro da tensão da corda.

Ou seja, a força sobre a polia que está mais próxima ao bloco de massa recebe o dobro desse peso!

Mas por enquanto, isso não vai fazer tanta diferença. Já que tem duas cordas segurando essa polia, elas vão dividir entre elas esse peso dobrado, e é como se cada uma das cordas estivesse segurando um bloco inteiro de massa .

Mas ainda não acabou! Repetindo a sugestão do enunciado: a força sobre a polia é o dobro da tensão da corda.

Isso quer dizer que a polia dá uma ajuda a mais pra levantar o bloco, de forma que a tensão mesmo sobre a corda é só metade desse peso:

Agora é só calcular a velocidade em cada uma das cordas.

(a) Na corda a velocidade vai ser:

(b) Já na corda a velocidade vai ser:

Maravilha, dessa vez, cada corda só tem uma polia presa em um bloco.

A gente viu que a polia “divide a força ao meio”, ou seja, ela só repassa metade da força sobre ela na forma de tração sobre a corda.

Então dessa vez, a tensão em cada corda vai ser simplesmente:

Então vamos calcular os valores das massas e para as velocidades serem iguais:

Belezoca, lembrando da fórmula:

No caso da corda (1):

E no caso da corda (2):

Igualando as duas:

Elevando tudo ao quadrado:

Logo:

E agora juntando com a outra informação que temos:

Chegamos em um sistema.

Iradoso, agora é só a gente resolver o sistema. Isolando na primeira relação, obtemos que:

Então substituindo esse resultado na segunda relação, vamos descobrir que:

Logo:

E agora substituindo isso na segunda equação, descobrimos que vale:

Prontinho!