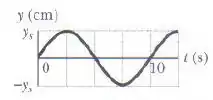
Uma onda transversal senoidal de comprimento de onda se propaga em uma corda no sentido positivo de um eixo . O deslocamento da partícula da corda situada em é dado na figura em função do tempo . A escala do eixo vertical é definida por . A equação da onda deve ser da forma . (a) Em o gráfico de em função de tem a forma de uma função seno positiva ou de uma função seno negativa? Determine (b) , (c) , (d) , (e) , (f) o sinal que precede e (g) a velocidade da onda. (h) Qual é a velocidade transversal da partícula em para ?

(a) A primeira pergunta não é sobre o gráfico dado na questão. É sobre o gráfico dessa função aqui:

E a pergunta é se esse gráfico é do mesmo tipo de uma função seno negativa ou positiva.

Bom, a amplitude sempre vai ter um valor positivo, já que é uma distância. Então a única coisa que poderia mudar a “cara” dessa função é a fase . Vamos calcular ela.

O gráfico do enunciado representa essa função:

Como a onda se propaga no sentido positivo, o sinal do é negativo (ver letra (f)).

Mas ele tem a “cara” de uma função seno positiva (começa crescente) e cruza o zero, ou seja:

A única forma de isso acontecer é se , porque nesse caso:

Usando a propriedade de soma na função seno:

E como :

Agora, finalmente, podemos responder a pergunta. Qual é a cara do gráfico da função a seguir?

Como acabamos de ver, somando a gente faz a o seno trocar de sinal. Então essa função tem o gráfico de uma função seno negativa.

(b) Lembrando que o gráfico do enunciado representa essa função aqui:

Pra achar a amplitude é só procurar a altura dos picos da onda. Olhando o gráfico, dá pra ver que:

(c) O valor de segue uma fórmula simples:

Usando o comprimento de onda que o enunciado deu:

(d) A frequência angular segue essa fórmula, entre tantas outras:

Então fica faltando apenas o período, que é o tempo que a função demora pra se repetir. Olhando o gráfico, dá pra ver que

(e) Já calculamos o valor de na letra (a), era:

(f) Também já analisamos o sinal que acompanha , seguindo esse macete:

Então no nosso caso, o sinal é negativo.

(g) A velocidade da onda também segue uma fórmula simples. Existem várias, mas vamos escolher uma que inclua só valores que já calculamos:

(h) Pra saber a velocidade transversal da partícula em e vamos ter que completar a função do deslocamento transversal:

E derivando em relação ao tempo pra achar a velocidade:

Como esse cosseno dá praticamente :