Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 16.1 - Ex. 6
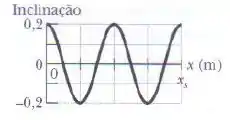
Uma onda senoidal se propaga em uma corda sob tensão. A Figura mostra a inclinação da corda em função da posição no instante . A escala do eixo é definida por . Qual é a amplitude da onda?
Passo 1
Belezera galerinha, vamos começar interpretando bem o gráfico. O enunciado disse que o eixo mostra a inclinação da corda em função da posição.
Essa é uma grandeza meio estranha, então vamos lembrar da função da onda antes:
Então, como chegamos na inclinação da corda em função da posição ()? Tiramos a derivada em relação à !
Como a função de onda tem duas variáveis, vamos tirar uma derivada parcial:
E o gráfico é só a representação disso em função de quando , ou seja:
Passo 2
Iradoso, agora que já entendemos o gráfico, vamos procurar o que a questão pediu: A amplitude da onda, ou seja, o valor de .
Bom, qual o valor máximo que a nossa função atinge? Como o cosseno varia entre e , o valor máximo vai ser:
Olhando o gráfico, dá pra ver que o máximo da função é igual a , ou seja:
Agora pra descobrir o valor de falta achar o .
Passo 3
Olhando o gráfico, dá pra gente ver que o comprimento da onda é , já que a escala do gráfico é .
Obs.: O comprimento de onda no gráfico não muda quando tiramos a derivada, já que o continua dentro da função trigonométrica.
Substituindo na fórmula do número de onda :
E voltando na fórmula de cima:
Ou em :
Resposta
A amplitude da onda é .