Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 15.1 - Ex. 21

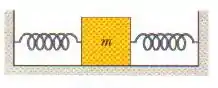
Na figura, duas molas estão presas a um bloco que pode oscilar em um piso sem atrito. Se a mola da esquerda é removida, o bloco oscila com uma frequência de 30   H z . Se a mola removida é a da direita, o bloco oscila com uma frequência de 45   H z . Com que frequência o bloco oscila se as duas molas estão presentes?

Passo 1

Então tá, vamos começar procurando uma fórmula pra frequência de um oscilador composto por um bloco e duas molas.

Se você se lembra bem da EDO que leva à função do oscilador harmônico, isso vai ser bem familiar. Vamos analisar as forças que agem sobre o bloco quando ele está preso nas duas molas.

Começando pela mola da esquerda: quando o bloco vai pra frente (direita), a mola puxa ele pra trás (esquerda), ou seja:

F e s q = - k 1 . x

Agora a mola da direita. Quando o bloco vai pra frente (direita), ele também empurra a mola pra trás (esquerda):

F d i r = - k 2 . x

Faz sentido, né? As duas molas querem manter o bloco onde ele está, então é compreensível que as forças tenham fórmulas iguais.

Agora colocando isso na segunda lei de Newton:

F = m a = F e s q + F d i r = - ( k 1 + k 2 ) . x

m a = - ( k 1 + k 2 ) . x

Passo 2

Agora você deve lembrar como isso vira uma EDO (equação diferencial ordinária).

A aceleração a ( t ) é simplesmente a derivada segunda do deslocamento x ( t ) , ou seja:

m . a ( t ) = - ( k 1 + k 2 ) . x ( t )

m . x ' ' t = - ( k 1 + k 2 ) . x ( t )

m . x ' ' t + ( k 1 + k 2 ) . x t = 0

Dividindo tudo pela massa:

x ' ' t + k 1 + k 2 m x t = 0

Agora, pra não ter que resolver a EDO (o que dá bastante trabalho) você tem que lembrar o seguinte, a EDO do oscilador harmônico segue essa fórmula aqui:

x ' ' t + ω 2 x t = 0

Onde esse ω é a frequência angular. Ou seja, olhando a nossa fórmula, dá pra ver que:

ω 2 = k 1 + k 2 m

ω = k 1 + k 2 m = k 1 m + k 2 m

Agora fica faltando achar esses valores de k 1 , k 2 e m .

Passo 3

A questão deu duas frequências de oscilação f 1 e f 2 , cada uma correspondente a uma mola, separadamente. Como a gente pode relacionar essas frequências às constantes elásticas das molas?

ω 1 = 2 π f 1 = k 1 m

ω 2 = 2 π f 2 = k 2 m

Beleza, agora vamos arrumar isso pra podermos substituir na equação lá de cima.

2 π f 1 2 = k 1 m

2 π f 2 2 = k 2 m

E agora substituindo:

ω = k 1 m + k 2 m = 2 π f 1 2 + 2 π f 2 2 = 2 π f 1 2 + f 2 2

Mas essa é a frequência angular, a frequência de oscilação vai ser:

f = ω 2 π

Ou seja:

f = 2 π f 1 2 + f 2 2 2 π = f 1 2 + f 2 2

Resultado sensacional, né? Bem legal. Essa é uma fórmula muito usada pra frequência de oscilações acopladas, em alguns livros é bastante discutida.

Agora substituindo:

f = 30 2 + 45 2 = 54   H z

Resolvido! Uma bela questão.

Resposta

Oscila com frequência f = 54   H z .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Na figura, duas molas são ligadas entre si e a um bloco de massa 0,245k g que oscila em um piso sem atrito. As duas molas possuem uma constante elástica k = 6430N / m . Qual é a frequência das oscilaç
(a) Estime o período natural de oscilações por balançar seus braços quando você anda, quando suas mãos estão vazias. (b) Agora estime o período natural de oscilação quando você está carregando uma mal
Durante um terremoto, um piso horizontal oscila horizontalmente em um movimento harmônico simples aproximado. Suponha que ele oscile em uma única frequência, com 0,80s de período. (a) Após o terremoto
Mostre que, nas situações mostradas na figura, o corpo oscila com uma frequência f = 1 2 π k e f m , onde k e f é dado por (a) k e f = k 1 + k 2 e (b) 1 / k e f = 1 / k 1 + 1 / k 2 . Dica: Determine a