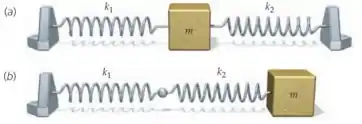
Mostre que, nas situações mostradas na figura, o corpo oscila com uma frequência , onde é dado por (a) e (b) . Dica: Determine a magnitude da força resultante sobre o corpo para um pequeno deslocamento e escreva . Note que na parte as molas são distensidas de quantidades diferentes, cuja soma é .
Passo 1
(a) Dê uma olhada na figura de cima. Quando a mola da esquerda sofre uma compressão por uma distância , a mola da direita sofre uma expansão por uma distância .
As duas molas fazem forças que favorecem o retorno do bloco à sua posição inicial, então:
Agora igualando isso a , conforme a sugestão do enunciado:
Então:
Passo 2
(b) Assim como, no item anterior, as duas molas sofriam a mesma deformação, neste item as duas molas experimentam a mesma força:
E essa é nossa primeira equação.
A deformação total da dupla de molas é , então:
Vamos substituir com uma das expressões que temos para :
E também substituir em função de :
Agora dividimos o numerador e o denominador por :
Que é exatamente o que queríamos demonstrar.
Resposta
Demonstração.