Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 12.2 - Ex. 23
Na figura, a extremidade de uma viga homogênea de de peso está presa por uma dobradiça a uma parede. A outra extremidade é sustentada por um fio que faz o mesmo ângulo com a viga e com a parede. Determine (a)a tensão do fio e as componentes (b)horizontal e (c)vertical da força que a dobradiça exerce sobre a viga.
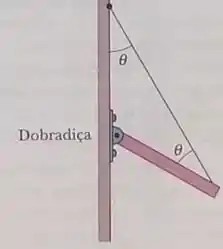
Passo 1
Belezera galerinha, na letra (a) como temos um problema de equilíbio estático, vamos identificar todas as forças que atuam sobre o sistema fazendo um diagrama de forças como o abaixo:
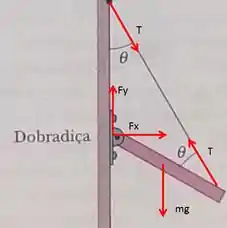
Uma estratégia boa para encontrarmos o valor pedido da tensão no fio é a gente verificar o equilíbrio de torques com relação a um ponto estrategicamente escolhido. Vamos escolher aqui a dobradiça como a localização desse ponto. Assim, temos:
Isolando :
Tal que é o comprimento da viga e o peso dela, que é igual a .
Passo 2
Substituindo os dados do enunciado nessa expressão de cima, a gente consegue obter o valor de , dado como:
Sendo assim:
Passo 3
(b) A malandragem aqui, é a gente usar a semelhança de triângulo, para verificar que o ângulo que a tensão faz com o eixo é extamente igual a , de forma que:
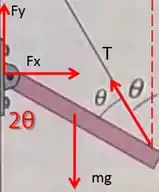
Dessa forma, para a tensão , obtemos que:
Passo 4
(c)Do equilíbrio vertical das forças mostradas acima, podemos encontrar:
Logo:
Resposta
(a)
(b)
(c)