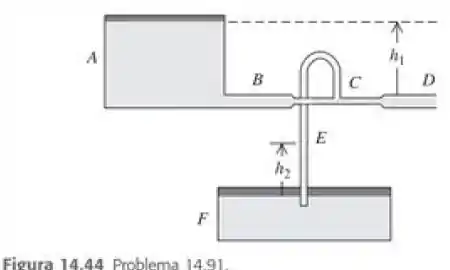
Dois grande tanques abertos A e F (Figura 14.44) contém o mesmo liquido. Um tubo horizontal BCD, que tem uma constrição C e é aberto ao ar no ponto D, sai da base do tanque A, e um tubo vertical E parte da constrição C e mergulha no liquido do tanque F. Suponha um escoamento com linhas de corrente e despreze a viscosidade. Sabendo que a área da seção reta da constrição C é a metade da área D e que D está a uma distancia abaixo do nivel do liquido no tanque A, até que altura o liquido subirá no tubo E? Expresse sua resposta em termos de .

A aplicação da equação de continuidade aos pontos em e diz que:

Onde:

• é a área transversal do cano no ponto C;
• é a velocidade do líquido no ponto C;
• é a área transversal do cano no ponto D;
• é a velocidade do líquido no ponto D que já conhecemos:

Sabe mais o que ele nos disse no enunciado? Que área da seção reta do ponto C é a metade da área D:

Então vamos substituir essa informação na nossa equação de continuidade? Olha só:

Substuindo o valor da velocidade no ponto D:

Vamos cortar dos dois lados da equação:

Passando esse 2 para dentro da raiz, vamos ter:

O que indica que a velocidade do fluido é de em .

Nós vamos considerar que a pressão no ponto E é a mesma pressão no ponto C, mas qual é a pressão no ponto C? Vamos usar a equação de Bernoulli entre os pontos que eu já conheço que são os pontos A e C:

Como o tanque A tem uma área muito maior do que a área no ponto C, podemos considerar que a velocidade do escoamento da água em A é praticamente nula:

Logo, essa simplificação na equação fica igual a:

Se consideramos que a altura do tanque é , logo estamos considerando o ponto C no nosso referencial zero, logo:

E nossa equação se reduz a:

Substituindo o valor da velocidade que encontramos do líquido no ponto C:

Fazendo essa conta temos:

Simplificando ficamos com:

Ai você me pergunta, mas como eu não tenho mais apenas a pressão no ponto C, também veio a pressão no ponto A. E eu te digo: Tenha calma, vamos chegar lá!

Concorda comigo que pelos dois tanques estarem abertos, tanto A quanto F, as pressões neles são iguais? Logo:

E nós já tínhamos falado que a pressão no ponto C é a mesma no ponto E:

Então vamos aplicar a equação de Bernoulli nos pontos E e F? Saca só:

Vamos considerar pelo mesmo motivo do tanque ser muito maior em F do que a área de passagem E que a velocidade de escoamento em F é:

Como a altura no ponto E não está aumentando, não temos uma velocidade naquele ponto, logo:

E ficamos com a equação:

E a diferença de altura entre os pontos F e E, não é a altura ? Então:

Como

E

Substituindo a equação :

Logo:

Pronto, chegamos na resposta!