Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Young and Freedman - Vol 4- Ed: 12º - Capítulo 36.Exercícios - Ex. 21

Na figura o máximo central da difração contém exatamente sete franjas de interferência e nesse caso d / a = 4 .

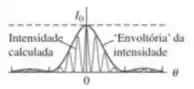
  1. Qual deve ser a razão d / a para que o máximo central de difração contenha exatamente cinco franjas?
  2. No caso considerado no item (a), quantas franjas há no primeiro máximo de difração existente de cada lado do máximo central?

Passo 1

Vamos lá! Podemos dizer que a localização da franja de interferência máxima é obtida através da relação

d   s e n θ = m λ     ( 1 )

onde m assume valores inteiros.

No caso, queremos o valor de m para que haja 5 franjas. Sendo assim

m =   ± 3     .

Passo 2

Precisamos descobrir o valor de θ para que

I = 0 .

Sabendo que a intensidade é dada por

I = I 0 s e n β 2 β 2 2

Onde

β = 2 π λ a   s e n θ   .     ( 2 )

Podemos perceber que I = 0 quando

s e n β 2 β 2 = 0

Isso nos dá que β precisa ser múltiplo de 2 π , vamos considerar que

β = 2 π .

Passo 3

Juntando (1) e (2), temos

β = 2 π λ a 2 λ d  

Como β = 2 π . Temos

d a = 3 .

Passo 4

m = ± 3 corresponde ao primeiro corresponde ao primeiro mínimo de difração. Precisamos agora obter o segundo mínimo. Para isto, temos que

β = 4 π .

Retornando um pouquinho vemos que

β = 2 π λ a 2 λ d

Substituindo β , temos

4 π = 2 π m 3 ⟹ m = 6

Para o primeiro máximo de difração em um lado contém m = ± 4 e m = ± 5 , sendo assim podemos escrever que temos duas franjas.

Resposta

a )     d a = 3 .

b )   2   f r a n j a s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

62. Difração dos raios X do sal. Raios X com 0,125n m de comprimento de onda são espalhados por uma rede cristalina cúbica (de um cristal de cloreto de sódio), cujo espaçamento entre átomos adjacentes
61. Diagrama de fasores para oito fendas. Uma figura de interferência é formada por oito fendas estreitas igualmente espaçadas. A Figura 36.14 mostra diagramas de fasores para os casos em que a difere
53. Considere uma figura de difração de fenda única. O centro do máximo central, cuja intensidade é igual a I 0 está localizado em θ = 0 . a ) Designe por θ + e θ - os dois ângulos de cada lado de θ =
59. Largura angular de um máximo principal. Considere N fendas estreitas igualmente espaçadas. Use a aproximação para ângulos pequenos sen ⁡ θ = θ (para θ em radianos) e mostre que, para um certo máxi
57. Uma fenda com largura de 0,360m m é iluminada por raios luminosos paralelos cujo comprimento de onda é 540n m . A figura de difração é observada sobre uma tela situada a uma distância de 1 , 20m d