Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 15.1 - Ex. 22
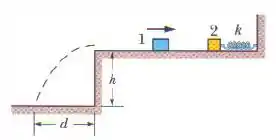
A figura mostra o bloco , de massa , deslizando para a direita, em uma superfície elevada, com uma velocidade de . O bloco sofre uma colisão elástica com o bloco , inicialmente em repouso, que está preso a uma mola de constante elástica . (Suponha que a mola não afeta a colisão.) Após a colisão, o bloco inicia um MHS com um período de e o bloco desliza para fora da extremidade oposta da superfície elevada, indo cair a uma distância horizontal dessa superfície, depois de descer uma distância . Qual é o valor de ?
Passo 1
Belezera galerinha, essa aqui é uma questão que mistura muitas coisas, então vamos ver o que realmente precisamos achar.
A ideia aqui é a gente encontrar o valor da distância que o bloco alcança depois que cai de uma altura de , certo? Pra isso, precisamos achar a velocidade do bloco no momento da queda, ou seja, a velocidade do bloco depois da colisão.
Então vamos usar as fórmulas que conhecemos da colisão elástica, o que é possível já que a questão pediu pra fingirmos que a mola não afeta a colisão. A fórmula bizurada para a velocidade final do bloco , pode ser dada como:
No nosso caso, a velocidade inicial do bloco é zero, então , dessa forma:
Iradoso. Temos quase tudo que precisamos pra achar a velocidade , só está faltando a massa do bloco . Vamos achar isso então.
Passo 2
Belejóia pessoal, a gente sabe que o bloco executa um MHS de período quando preso em uma mola de constante elástica .
Ou seja, usando a fórmula da frequência angular:
E agora elevando tudo ao quadrado e isolando a massa nessa equação:
Logo:
Substituindo os valores que o enunciado forneceu pra gente:
Beleza, agora voltando pra fórmula lá de cima da velocidade:
Obtemos que:
O menos apareceu porque antes da colisão o bloco ia pra direita, e depois passou a andar pra esquerda. Mas já que podemos escolher qualquer referencial, vamos pegar só o módulo.
Passo 3
Agora na volta do bloco , temos que o movimento vira só uma questão de lançamento oblíquo, onde o trajeto é dada como:
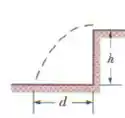
Temos um bloco que faz essa trajetória aí, com velocidade inicial , e sabemos ambém que .
Primeiro, precisamos saber quanto tempo o bloco leva até tocar o chão, pra isso usamo a equação:
Como a velocidade inicial é toda na horizontal, , além disso, e . Então:
Pronto, esse é o tempo que o bloco leva na queda. Agora a dustância que ele percorre nesse tempo, é dada como
Portanto:
Pronto!
