Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 15.1 - Ex. 5
Em um barbeador elétrico a lâmina se move para frente e para trás, ao longo de uma distância de , em um movimento harmônico simples com uma frequência de . Determine (a) a amplitude, (b) a velocidade máxima da lâmina e (c) o módulo da aceleração máxima da lâmina.
Passo 1
Fala galerinha bonita, show de bolinhas com vocês?
Saca só, nesse exercício aqui a gente pode ser malandro e escrever a equação do oscilador, e depois tirar todas as respostas dela. Desse modo, a equação da posição angular é dada como:
Pra montar a equação já somos obrigados a resolver a letra (a), que pede a amplitude do oscilador.
O deslocamento total do barbeador é , e sabemos que a amplitude é sempre a metade do deslocamento total. Isso quer dizer que a amplitude é metade do comprimento desse arco pontilhado que representa a trajetória.
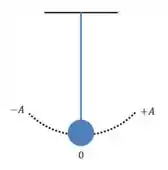
Ou seja:
E essa já é a resposta da letra (a).
Agora pra gente ir para letra (b), vamos primeiro só achar achar a frequência angular , dada como:
Logo:
E agora chegamos na equação final da posição:
Passo 2
Iradoso, agora vamos lá, a letra (b) pede a velocidade máxima do oscilador.
Pra achar a função da velocidade, é só derivar a equação da posição em relação ao tempo:
Dessa maneira, obtemos que:
Como o seno varia entre e , o valor máximo dessa função da velocidade vai ser:
E essa é a resposta da letra (b).
Passo 3
Agora pra achar a função que dá a aceleração, é só derivar de novo essa função:
De modo que:
A função cosseno também varia entre e ,então o valor máximo que a aceleração assume é:
Pronto, essa é a resposta da letra (c).
Resposta
(a)
(b)
(c)