Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 16.1 - Ex. 8
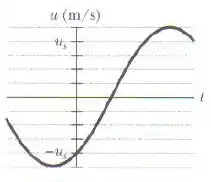
A figura mostra a velocidade transversal em função do tempo para o ponto de uma corda situado em , quando uma onda passa por ele. A escala do eixo vertical é definida por . A onda tem a forma . Qual é o valor de ?
(Atenção: As calculadoras nem sempre fornecem o valor correto de uma função trigonométrica inversa; por isso, verifique se o valor obtido para é o valor correto, substituindo-o na função , usando um valor numérico qualquer para e plotando a função assim obtida.)
Passo 1
Falaa galerinha bonita, tudo beleza?
Nesse exercício aqui, o enunciado nos deu uma figura que mostra a velocidade transversal em função do tempo para o ponto de uma corda situado em , quando uma onda passa pelo ponto.
E sabendo que a escala do eixo vertical é definida por e que a onda tem a forma , o enunciado pede pra gente determinar o valor da constante de fase .
Belezoca, é importante entender bem o seguinte: esse gráfico inteiro é referente a um único ponto em uma corda, o ponto .
O valor que aparece no eixo é a velocidade transversal desse único ponto. Que valor é esse na nossa equação da onda?
Bom, quando a equação fica:
E a velocidade transversal é a derivada disso em relação ao tempo:
Essa é a função que está representada no gráfico.
Passo 2
Então agora vamos usar o gráfico pra ver as informações que temos sobre essa função.
Primeiro, olhando o ponto máximo que a função atinge no gráfico (, podemos afirmar que:
Já que o valor máximo que a função assume é , dado que o cosseno só varia entre e .
Então, por enquanto, nossa função está assim:
Segundo, olhando o ponto em que a função cruza o eixo , temos que:
Logo:
Então se a gente isolar , obtemos:
E jogando esse valor em uma calculadora, o resultado é:
Como deve estar no terceiro ou no quarto quadrante, a opção correta é que corresponde a um ângulo de , e portanto, está no quarto quadrante. Enquanto que corresponde a um ângulo de contido no primeiro quadrante. Sendo assim, a constante de fase será:
Resposta