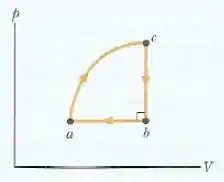
A figura mostra um ciclo fechado a que um gás é submetido. De até , deixam o gás na forma de calor. De até , deixam o gás na forma de calor e o valor absoluto do trabalho realizado pelo gás é . De até , são recebidos pelo gás na forma de calor. Qual é o trabalho realizado pelo gás de até ? (Sugestão: é preciso levar em conta os sinais dos dados fornecidos)

Vamos aplicar a primeira lei ao ciclo completo! Isso é bom porque aí podemos definir o valor da energia interna, olha só:

Se o ciclo começa e termina no mesmo ponto: qual a variação da energia interna? Exatamente, é zero! Ela não tem como variar se ela começa e termina no mesmo lugar.

Ou seja:

Ah ótimo, então se a questão pediu o trabalho, a gente pode calcular só o calor que dá no mesmo. (No ciclo completo)

Vamos fazer isso então.

Qual foi o calor total recebido pelo gás nesse ciclo todo?

De até , o enunciado diz que deixam o gás, ou seja, ele na verdade não recebeu nada, ao contrário, perdeu! Isso a gente representa com um sinal negativo:

De até , o gás perdeu mais :

E de até , o gás recebe (agora sim, é positivo) de calor:

Ou seja, o calor total recebido no ciclo completo foi:

E pela equação que a gente achou antes, isso quer dizer que o trabalho realizado pelo gás também foi de .

Então tá, no ciclo completo:

Esse trabalho total é a soma dos trabalhos nos três processos, concorda?

O enunciado já deu o valor desse segundo trabalho. Mas deu em módulo! Pra descobrir o sinal temos que ver o seguinte: o volume está aumentando? Então é positivo. Se estiver diminuindo, o trabalho é negativo. Nesse caso (na trajetória ) está diminuindo, então:

Mas olha só, o trajeto não é uma linha vertical? Ou seja, ele não é um processo a volume constante? Pois é, então o trabalho realizado ali é zero!

E então fica fácil achar o que pediram:

Ou seja: