Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 14.7 - Ex. 72
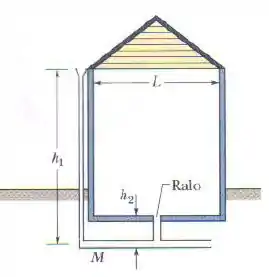
A figura mostra um diagrama muito simplificado do sistema de drenagem de água da chuva de uma casa. A chuva que cai no telhado inclinado escorre para as calhas da borda do telhado e desce por canos verticais (apenas um é mostrado na figura) para um cano principal abaixo do porão, que leva a água para um cano ainda maior, situado no subsolo. Na figura, um ralo no porão também está ligado ao cano . Suponha que as seguintes condições são verdadeiras:
- os canos verticais têm um comprimento ;
- o ralo do porão fica a uma altura em relação ao cano ;
- o cano tem um raio de ;
- a casa tem de fachada e de profundidade;
- toda água que cai no telhado passa pelo cano ;
- a velocidade inicial da água nos canos verticais é desprezível;
- a velocidade do vento é desprezível (a chuva cai verticalmente)
Para que índice de precipitação, em centímetros por hora, a água do cano chega à altura do ralo, ameaçando inundar o porão?
Passo 1
Show de bolinhas pessoal, tudo belezinha com vocês?
Nesse exercício aqui, temos um diagrama bem feio, mas vamos focar na pergunta: qual índice de precipitação da chuva permite que a água do cano chegue ao topo do ralo?
Outra forma de perguntar isso é: Quão rápido a água tem que estar fluindo pelo cano pra fazer com que a altura da água chegue ao topo do ralo?
Vamos supor que todo o cano está preenchido por água, e chamar de o ponto no topo da calha e de o ponto, no cano , logo abaixo do ralo. Podemos comparar os dois pontos usando a equação de Bernoulli:
Passo 2
A pressão no topo da calha é simplesmente a pressão atmosférica, e a pressão no ponto abaixo do ralo é a pressão atmosférica somada à pressão da coluna de água que preenche o ralo, ou seja:
Substituindo isso na equação:
E a velocidade em cada um dos pontos? No topo da calha pode ser considerada zero (lembrando que estamos considerando o cano preenchido), e no cano é a que queremos calcular:
A altura também pode ser considerada como zero, e a
E isolando a velocidade :
Então a velocidade no cano vai ser:
Precisamos agora ver a qual precipitação isso equivale.
Passo 3
O enunciado diz que a água cai no telhado e, logo em seguida, escorre para dentro da calha e depois para o cano . Podemos igualar as vazões de todos esses pontos.
Mas pra resolver a questão, o mais importante é ver o telhado (sobre o qual queremos calcular a precipitação) e o cano (onde já calculamos a velocidade da água):
Vamos calcular as duas áreas, começando pelo cano :
E a área do telhado (lembrando que temos que considerar o telhado todo, porque o enunciado avisou que tem mais uma calha no sistema):
Essa não é a área de superfície do telhado, é a área da região de onde a água vai para o telhado. Como se fosse a área desse retângulo imaginário “captando” a água que cairia no telhado:
Agora a equação da continuidade lá em cima fica assim:
E a velocidade com que a chuva cai no telhado é:
Convertendo isso para centímetros por hora, sabendo que uma hora tem :
Resposta
A precipitação deve ser de .