Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 19.9 - Ex. 59
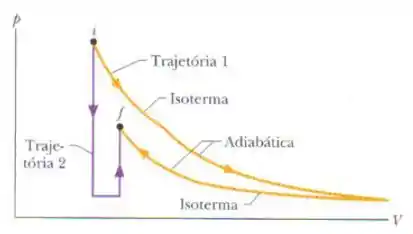
A figura mostra duas trajetórias que podem ser seguidas por um gás de um ponto inicial até um ponto final . A trajetória consiste em uma expansão isotérmica (o módulo do trabalho é ), uma expansão adiabática (o módulo de trabalho é ), uma compressão isotérmica (o módulo do trabalho é ) e uma compressão adiabática (o módulo do trabalho é ). Qual é a variação da energia interna do gás se ele vai do ponto para o ponto seguindo a trajetória ?
Passo 1
Bom, a primeira coisa que precisamos lembrar é que a variação da energia interna é independente do caminho! Isso quer dizer que só depende do ponto inicial e do ponto final, nesse caso, os pontos e .
Beleza, depois disso é só pensar na primeira lei da termodinâmica:
Vamos então analisar tudo pela trajetória .
O objetivo é simples: achar a variação da energia interna em cada trecho.
Passo 2
Nos trechos onde a transformação é isotérmica, a variação da energia interna é zero! Isso porque dá pra provar que a energia interna de um gás só depende da temperatura.
Passo 3
Então fica faltando só achar nos trechos adiabáticos! Mas olha, a própria definição da transformação adiabática garante que, nesses casos:
Ou seja:
Então é só somar os trabalhos nos trechos adiabáticos:
O enunciado só deu os módulos, então pra saber o sinal do trabalho temos que usar a seguinte regra:
Então beleza:
Pronto, essa é a variação da energia interna!
Resposta
A variação ao longo da trajetória é .