Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 15.Problemas Adicionais - Ex. 106

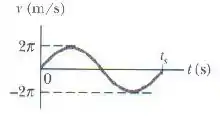
Um oscilador harmônico simples é formado por um bloco preso a uma mola com k = 200   N / m . O bloco desliza em uma superfície sem atrito, com o ponto de equilíbrio em x = 0 e uma amplitude de 0,20   m . O gráfico da velocidade v do bloco em função do tempo t aparece na figura. Qual é (a) o período do MHS, (b) a massa do bloco, (c) o deslocamento do bloco no instante t = 0 , (d) a aceleração do bloco no instante t = 0,10   s e (e) a energia cinética máxima do bloco?

Passo 1

(a) A questão envolve um oscilador harmônico bem simples: um bloco de massa m preso a uma mola de constante k = 200   N / m .

A primeira coisa que a gente precisa fazer é achar o período do movimento. Infelizmente a questão não a escala do eixo x no gráfico, então vamos ter que achar outro jeito.

Uma coisa que temos é a velocidade máxima do oscilador:

v m á x = 2 π   m / s

Beleza, essa já é uma fórmula que a gente conhece:

v m á x = 2 π = x m ω

Que também pode ser escrita em termos do período, já que   ω = 2 π / T .

2 π = x m . 2 π T  

Ou seja:

T = x m 2 π 2 π

E a amplitude x m já foi dada no enunciado!

T = 0,20   s

Passo 2

(b) Agora queremos saber a massa do bloco. Sem problemas, é só usar aquela famosa fórmula:

ω = k m

E como ω = 2 π / T :

2 π T = k m

E elevando tudo ao quadrado:

4 π 2 T 2 = k m

m = k T 2 4 π 2

m = 200 0,20 2 4 π 2 = 0,20   k g

Beleza, vamos em frente.

Passo 3

A letra (c) é uma pergunta legal: qual é o deslocamento do oscilador no ponto t = 0 ?

O gráfico que a questão deu é da velocidade, ou seja, da derivada do deslocamento:

v t = x ' ( t )

Olhando o gráfico, a gente vê que v 0 = 0 , então:

x ' 0 = 0

Ou seja: o ponto t = 0 é um ponto crítico da função do deslocamento! É um ponto de máximo ou ponto de mínimo.

Qual grandeza representa os máximos/mínimos da função deslocamento? Exatamente, a amplitude! O problema agora é saber se estamos no máximo x m = 0,20 ou no mínimo x m = - 0,20 .

Bom, se a gente pensar na derivada do gráfico no ponto t = 0 (ou seja, na aceleração, que é a derivada da velocidade), ela também é positiva, porque a função é crescente. Então:

a > 0

E como a lei de Hooke diz que:

m a = - k x

Quando a é positivo, x é negativo, então ali temos um ponto de mínimo do deslocamento.

x 0 = - 0,20   m

Passo 4

(d) Agora queremos a aceleração do gráfico no instante t = 0,10   s .

Bom, como falamos ali em cima, a aceleração é a derivada da função no gráfico da questão, já que:

a t = v ' ( t )

O problema é: onde está o ponto t = 0,10   s ?

Antes, tínhamos calculado que o período é T = 0,20   s . Como período é o tempo que a função leva pra se repetir, podemos dizer que aquele t s que foi marcado no gráfico é 0,20   s .

Ou seja, o ponto t = 0,10   s vai estar exatamente na metade desse intervalo. Olhando o gráfico, dá pra ver que estamos falando desse ponto aqui:

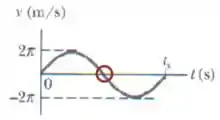
Ou seja, é o ponto de inclinação máxima do gráfico! Então:

a 0,10 = - a m á x

Obs.: É negativo porque a função é decrescente naquele ponto!

E a fórmula da aceleração máxima é:

a m á x = - x m ω 2

a ( 0,10 ) = - 0,20 k m 2 = - 0,20 200 0,20 = - 2,0   .   10 2   m / s 2

Pronto!

Passo 5

(e) Pra terminar, queremos a energia cinética máxima do bloco.

A fórmula da energia cinética é:

K = 1 2 m v 2

E a energia cinética vai ser máxima quando a velocidade for máxima!

Olhando o gráfico, a velocidade máxima é v m á x = 2 π   m / s , então:

K = 1 2 0,20 2 π 2 = 4,0   J

Resolvido!

Resposta

(a) T = 0,20   s

(b) m = 0,20   k g

(c) x 0 = - 0,20   m

(d) a 0,10 = - 2,0   .   10 2   m / s 2

(e) K = 4,0   J

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

32. Um gato com massa igual a 4,0k g está preso por arreios a uma mola ideal de massa desprezível e oscila verticalmente em M H S . A amplitude do movimento é 0,050m . No ponto mais alto do movimento,
31. Um corpo de 175g sobre um trilho de ar horizontal, sem atrito, é preso a uma mola fixa ideal de constante 155N / m . No instante que você efetua medições sobre o corpo, ele estará se movendo a 0,8
33. Uma bola de 1,50k g e outra de 2,0k g são coladas uma na outra, a mais leve embaixo da mais pesada. A bola de cima é presa mola vertical de constante 165N / m e o sistema está vibrando verticalmen
Um temor de terra coloca em vibração no sentido vertical, com frequência angular ω = 20 s - 1 e amplitude de 4c m , uma plataforma horizontal, sobre a qual está colocado um bloquinho de madeira. A pla
A energia total de um sistema conservativo na vizinhança de um equilíbrio estável é da forma E = a q ˙ 2 + ω 2 q 2 , onde q (deslocamento, ângulo, … ) é o desvio do equilíbrio e a e ω são constantes.