A figura mostra uma massa de colocada sobre uma massa de que oscila sobre uma superfície sem atrito. A constante elástica é de , e o coeficiente de atrito estático entre os dois blocos é de . Qual é a amplitude de oscilação máxima de movimento para que o bloco de cima não escorregue?
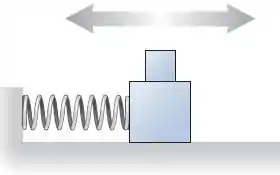
Passo 1
Se liga! Aqui temos que observar que o que faz o bloco de cima não escorregar é justamente a força de atrito entre ele e o bloco de baixo. A magnitude da força de atrito entre os dois blocos, tendo em vista que o movimento deles é horizontal, é dada por
A máxima força de atrito pode ser obtida usando . Substituindo os valores, considerando , temos
Passo 2
Considerando que quando todo o conjunto se move, o bloco de cima se move com uma aceleração e a única força que atua sobre ele no sentido do movimento é a própria força de atrito, podemos aplicar a 2ª Lei de Newton
Esta é a máxima aceleração que o sistema pode ter para o bloco de cima não escorregar.
Passo 3
Como nosso interesse é a amplitude, devemos usar a relação entre amplitude máxima e aceleração máxima.
Para resolver precisamos descobrir a frequência angular.
Onde representa a massa total do sistema
Portanto
Agora só precisamos substituir os valores para achar que a amplitude máxima é