Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 15.Problemas Adicionais - Ex. 108
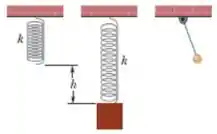
A figura mostra que, se pendurarmos um bloco na extremidade de uma mola de constante elástica , a mola sofrerá um alongamento . Se puxarmos o bloco ligeiramente para baixo a partir da posição de equilíbrio e depois o liberarmos, ele oscilará com certa frequência. Qual deve ser o comprimento de um pêndulo simples para que oscile com a mesma frequência?
Passo 1
Queremos que a mola e o pêndulo oscilem com a mesma frequência. Vamos lembrar das fórmulas para as frequências de oscilação da mola e do pêndulo:
Aqui estamos usando as frequências angulares, mas poderiamos usar a frequência em Hertz sem problemas.
Essa fórmula nos diz que, para que um pêndulo tenha a mesma frequência de uma mola, o seu comprimento deve ser:
Passo 2
Como podemos calcular essa última razão? Sabemos que é o valor da massa presa à mola e é a constante elástica.
A única outra informação que temos é que a massa produz uma deformação na mola. O que isso quer dizer?
Bom, se o bloco atinge o equilíbrio quando a mola atinge essa deformação, então nesse ponto temos a seguinte igualdade:
Que é exatamente a razão que encontramos no primeiro passo, então:
Resposta
O pêndulo deve ter um comprimento de .