Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 8.Problemas Adicionais - Ex. 132
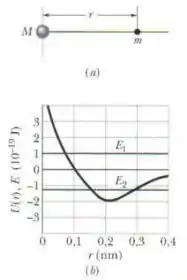
A figura a mostra uma molécula composta por dois átomos de massa e (com ) separados por uma distância . A figura b mostra a energia potencial da molécula em função de . Descreva o movimento dos átomos (a) se a energia mecânica total do sistema é maior que zero (como ) e (b) se é menor que zero (como ). Para e , determine (c) a energia potencial do sistema, (d) a energia cinética total dos átomos e (e) a força (módulo e orientação) que atua sobre cada átomo. Para que valores de a força é (f) repulsiva, (g) atrativa e (h) nula?
Passo 1
Para interpretar o gráfico na figura , pense o seguinte: o sistema só pode estar em pontos que ficam abaixo da linha da energia.
(a) No caso da energia , o sistema pode ficar apenas entre e .
Além disso, a reta cruza o gráfico aproximadamente em . Isso quer dizer que, nesse caso, os átomos se aproximariam até esse valor de , e depois começariam a se afastar até .
Passo 2
(b) No caso , os átomos estarião “aprisionados” entre os dois pontos em que a reta intersecta o gráfico.
Ou seja, os gráficos ficariam oscilando entre e :
Se não houver perda de energia (que na realidade sempre há), esse movimento se repetiria para sempre.
Passo 3
(c) Se e , como podemos calcular a energia potencial do sistema?
Na verdade o valor de não interfere nesse primeiro resultado, podemos apenas olhar para o gráfico em e ver que o valor de é próximo de:
Passo 4
(d) Para encontrar a energia cinética total dos átomos, é só lembrar do seguinte:
Passo 5
(e) Como encontrar a força a partir da energia potencial:
Mas como queremos o módulo da força:
Ou seja, temos que fazer uma estimativa para a inclinação do gráfico em para calcular essa força.
Mais cedo, nós disssemos que quando , Como aquele trecho do gráfico é muito próximo de uma reta, vamos pegar um ponto vizinho:
Então a inclinação da reta é:
Essa é uma estimativa bem “grosseira”, mas é o melhor que podemos fazer nesse caso.
Como nesse instante a inclinação é positiva, então a força tem sinal negativo, ou seja, ela faz com que diminua. Por isso ela age no sentido de aproximar os dois átomos.
Passo 6
(f) A força é repulsiva (sinal positivo, pois aumenta o valor de ), quando a inclinação do gráfico é negativa.
Isso acontece em .
Passo 7
(g) A força é atrativa (sinal negativo, pois diminui o valor de ), quando a inclinação do gráfico é positiva.
Isso acontece em .
Passo 8
(h) A força é nula apenas quando estamos sobre os pontos críticos do gráfico, ou seja, quando a inclinação é nula.
Isso acontece apenas no ponto de mínimo local em .
Resposta
(a) Haveria um ponto de retorno em , e outro no infinito.
(b) Haveria pontos de retorno nos dois pontos em que a reta cruza o gráfico.
(c) A energia potencial é próxima de .
(d) A energia cinética é .
(e) O módulo da força é , e age no sentido de atrair os átomos.
(f) A força é repulsiva para .
(g) A força é atrativa para .
(h) A força é nula para .