Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Randall D. Knight- Ed: 2º - Capítulo 14.Exercícios e Problemas - Ex. 32

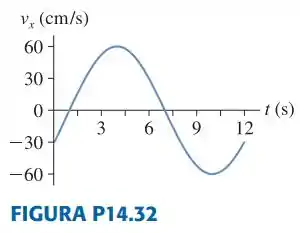
A FIGURA P14.32 é o gráfico velocidade versus tempo de uma partícula em movimento harmônico simples.

a. Qual é a amplitude da oscilação?

b. Qual é a constante de fase?

c. Qual é a posição para t =   0   s ?

Passo 1

Se atente que o gráfico dado é da velocidade, não da posição como na questão anterior.

E a amplitude da velocidade é de 60   c m / s sendo essa a velocidade máxima da partícula, portanto:

v m á x = A ω

Com ω = 2 π T = 2 π 12 = π 6 , uma vez que o período dessa onda é de 12   s . Então a amplitude da oscilação será de:

A = v m á x ω = 60 × 10 - 2 π 6 = 114.6   c m

Passo 2

E pelo gráfico podemos dizer que a equação da velocidade será de:

v = - 60   s e n π 6 t + ϕ 0   c m s

A equação v = - ω A   s e n ( ω t + ϕ 0 ) tem que ser respeitada em toda a sua forma.

Então como sabemos que a velocidade inicial é de - 30     c m / s então para t = 0 temos:

- 30 = - 60   s e n ( ϕ 0 )

s e n ϕ 0 = 1 2

ϕ 0 = s e n - 1 1 2 = π 6   o u 5 π 6

Como a velocidade inicial é negativa (então ela está na metade de cima do círculo) e está diminuindo (está no segundo quadrante) então ϕ 0 = 5 π 6

v = - A ω   s e n ω t + ϕ 0

Passo 3

Dessa forma podemos escrever a equação da posição:

x = A   c o s ⁡ ( ω t + ϕ 0 )

x = 114.6 cos ⁡ π t 6 + 5 π 6 [ c m ]

Para t = 0 teremos:

x = 114.6 cos ⁡ 5 π 6 = - 99.25   c m

Resposta

a )   114.6   c m

b )   ϕ 0 = 5 π 6   r a d

c ) - 99.25   c m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A figura ( a ) é um gráfico parcial da função posição x ( t ) de um oscilador harmônico simples com uma frequência angular de 1,20r a d / s ; a figura ( b ) é um gráfico parcial da função velocidade v
A Fig. 15-51 mostra a posição x t de um bloco que oscila em um MHS na extremidade de uma mola t s = 40,0 m s . Qual é (a) a velocidade e (b) o módulo da aceleração radial de uma partícula no movimento
Qual é a constante de fase do oscilador harmônico cuja função aceleração a(t) aparece na Fig. 15-55 se a função posição x(t) é da forma x = x m c o s ω t + ϕ e a s = 4,0 m / s 2 ?
17. Sobre um trilho de ar sem atrito, horizontal, um corpo oscila na extremidade de uma mola ideal de constante 2,50N / c m . O gráfico da Figura 13.31 mostra a aceleração do corpo em função do tempo.
Ache o movimento resultante de dois movimentos harmônicos simples na mesma direção dados por: x 1 = cos ⁡ ω t - π 6 , x 2 = sen ⁡ ω t . Represente graficamente os respectivos vetores girantes.