Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 15.1 - Ex. 20
A figura é um gráfico parcial da função posição de um oscilador harmônico simples com uma frequência angular de ; a figura é um gráfico parcial da função velocidade correspondente. As escalas dos eixos verticais são definidas por e . Qual é a constante de fase do MHS se a função posição é dada na forma ?
Passo 1
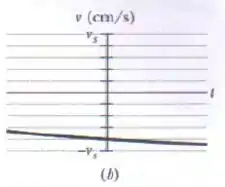
Então, o gráfico da esquerda representa um pequeno trecho dessa função aqui:
E o gráfico da direita, que representa a velocidade do oscilador, é simplesmente a derivada dessa função (porque a velocidade é a derivada da posição em relação ao tempo):
Olhando os pontos em que as funções cruzam o eixo , dá pra identificar as seguintes igualdades:
Também foi dito que . Vamos juntar tudo isso em um sistema:
Passo 2
Nosso objetivo é encontrar a constante de fase . Uma boa opção (muito usada pra resolver sistemas envolvendo funções trigonométricas) é dividir a segunda equação pela primeira:
Passo 3
E agora a solução do problema está nessa equação aqui:
Jogando isso em uma calculadora científica (que esteja em modo radianos), achamos:
Somando a esse valor pra achar outro ângulo com a mesma tangente:
E existem outras infinitas soluções, essas só são as únicas entre e . Nesse caso é melhor deixar a resposta em termos da tangente inversa mesmo.
Resposta