Enunciado
Física - Moysés - Vol. 2 - Ed: 4º - Capítulo 3.Problemas - Ex. 24
Ache o movimento resultante de dois movimentos harmônicos simples na mesma direção dados por: , . Represente graficamente os respectivos vetores girantes.
Passo 1
Vamos começar escrevendo as duas funções como cossenos. Para isso é só lembrar da seguinte propriedade:
Então:
O que essas equações dizem? Que nós podemos pensar nesses deslocamentos como as componentes horizontais de dois vetores girantes (fasores) com frequência e amplitude .
Dê uma olhada no desenho:
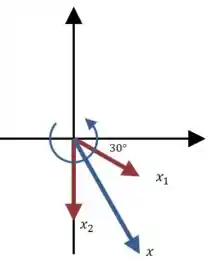
E o vetor resultante é a soma vetorial de e .
Passo 2
As amplitudes de e são:
Então, usando a fórmula para a soma de fasores:
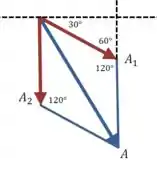
Então até agora temos a seguinte expressão para o deslocamento resultante:
Falta determinar a fase.
Passo 3
Para encontrar a fase só precisamos determinar o ângulo que o vetor forma com o eixo horizontal no instante inicial.
Vamos destacar um triângulo naquele mesmo desenho do passo anterior:
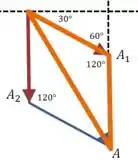
Esse triângulo é isósceles, porque os dois lados que formam o ângulo de são iguais:
Isso quer dizer que os dois outros ângulos do triângulo são iguais:
E então o ângulo que o vetor resultante forma com a horizontal é:
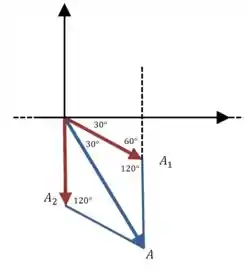
Então a função que estávamos procurando é:
Resposta
O movimento resultante é .