1. Show de bola pessoal, esse exercício precisa de um pouco da nossa atenção!! Vamos analisar toda a situação a partir da expressão de módulo do torque , dada como:

Onde é a força, é o tamanho do braço de alavanca e é o ângulo aplicado.

Pois vamos analisar o torque com uma força aplicada em diferentes distancias e direções da origem.

Vamos imaginar que a barra esteja sobre o eixo e essa seja a distância da extremidade esquerda da barra em que a corda está presa, lembrando a extremidade direita está na origem.

O nosso diagrama fica assim:



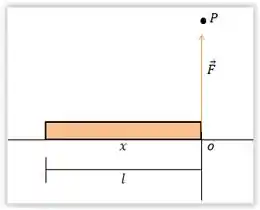
Como a força é direcionada ao ponto , formando um ângulo de , o torque será máximo no final da haste, uma vez que pela fórmula do torque e são grandezas diretamente proporcionais. Opa, já respondemos a letra (a).



Passo 3

2. Utilizando a mesma relação do item (a), se o ponto estiver situado acima da extremidade esquerda da barra, temos a seguinte representação:



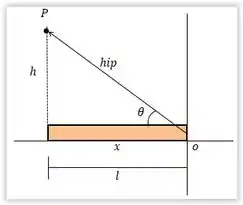
Vamos calcular o ângulo pelo seno:

Substituindo na fórmula:

Masss, como temos um triangulo retângulo, pelo teorema de Pitágoras, sabemos que:



Logo:

Para que essa função tenha valor máximo, precisamos que:

portanto, a extremidade direita apresenta o torque máximo.

Passo 4

3. Já para o centro da barra, temos a seguinte representação:

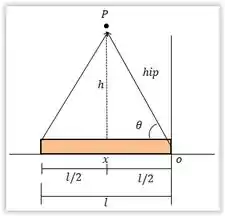
Fazemos da mesma forma do item (b), calculando o seno:

Substituindo:

Masss, como temos um triangulo retângulo, pelo teorema de Pitágoras:

Logo,

Analisando essa fórmula para determinarmos onde o é máximo, vemos que existem dois modos para aumentar o torque: aumentando o comprimento da alavanca e aumentando .

Assim, para encontrar um em que apresenta o ponto máximo, temos que diferenciar em relação a . Logo:

Prontinho!!