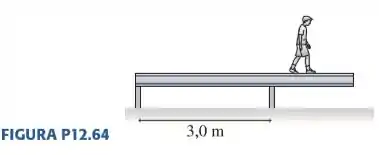
Uma viga de e de comprimento é sustentada, sem estar fixada, pelas duas pilastras mostradas na FIGURA P12.64. Um garoto de começa a caminhar ao longo da viga. Quão próximo ele pode chegar da extremidade direita da viga sem que ela tombe?
Passo 1
Bom, à medida que o garoto anda para a extremidade direita da viga, ele se distancia do segundo suporte, que será o eixo de rotação quando a viga girar. Quanto mais ele se distancia, maior é o efeito do torque já que:
A força é o peso do rapaz, e ela é constante durante todo o processo, mas se a distância aumentar o torque aumenta também, e isso pode causar rotação na viga se o peso da viga não for suficientemente grande. Como estamos numa situação de iminência, a força normal produzida pelo primeiro suporte é muito próxima de zero.
Passo 2
Vamos calcular até onde o garoto pode andar na viga sem que ela vire, para isso, precisaremos da segunda lei de Newton para o caso rotacional:
O lado direito precisa ser zero porque não queremos que a viga rotacione.
Se a gente considerar que o sentido anti-horário é o sentido positivo de rotação, o peso da barra produz um torque no sentido anti-horário e o peso do menino no sentido horário:
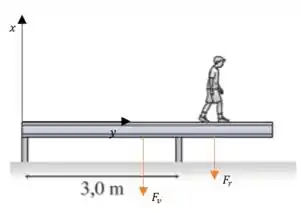
A soma dos torques então fica:
Sendo que se refere ao rapaz e à viga.
Passo 3
Agora calculamos o peso de cada um e a distância do centro de massa da viga até o ponto onde está o eixo de rotação:
O que fizemos na última equação foi: pegamos a posição do eixo, , e subtraímos esse valor pela posição do centro de massa da viga, que está exatamente no meio da viga, como ela tem de comprimento, a posição do centro de massa tem que ser .
Passo 4
Então é só isolar que é a distância na viga que o rapaz pode ficar em relação ao eixo:
E substituir cada valor:
Até de distância do eixo, o garoto pode andar sem que a viga tombe, como o enunciado pede a distância em relação à extremidade direita então:
é a distância mais próxima da extremidade direita que o garoto pode chegar.