Uma fina lâmina quadrada e condutora tem bordas com de comprimento e uma carga resultante de . (Considere que a carga esteja uniformemente distribuída nas faces da lâmina). (a) Determine a densidade de carga em cada face da lâmina e o campo elétrico nas proximidades de uma face. (b) A lâmina está colocada à direita de um plano infinito, não condutor e carregado, com densidade de carga igual a , com as faces da lâmina paralelas ao plano. Determine o campo elétrico em cada face da lâmina e determine a densidade de carga em cada face.

1. Cada face receberá metade da carga dada para a lâmina. Sendo assim, temos que
2. O segredo aqui é sacarmos que o campo no interior de nossa lâmina deve ser zero. Veja a figura a seguir.

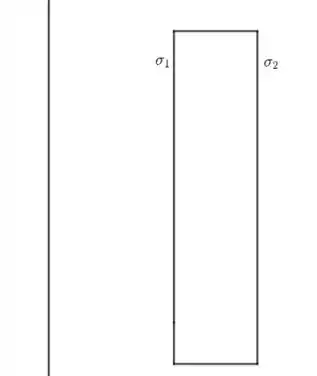
Suponha que e sejam positivas. Dessa forma, como o campo elétrico no interior da lâmina, temos que

Porém, notemos que

Portanto, temos o sistema de equações:

Se somarmos as duas equações, teremos

De forma que