Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 11.Problemas - Ex. 86

Um fio metálico, que possui comprimento de 3,50 m e diâmetro igual a 0,70 mm, foi submetido ao seguinte teste. Uma carga pesando 20 N foi inicialmente presa ao fio para mantê-lo esticado. A posição da extremidade inferior do fio foi medida com uma régua enquanto a carga aumentava.

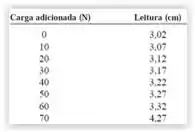
a) Faça um gráfico desses valores, plotando o aumento do comprimento no eixo horizontal e o aumento da carga no eixo vertical.

b) Calcule o valor do módulo de Young.

c) O limite de proporcionalidade é atingido quando a leitura da régua indica 3,34 cm. Qual era a tensão nesse ponto?

Passo 1

Vamos pegar a fórmula do módulo de elasticidade e manipular hehe.

F ⊥ = Y A ∆ l l 0

Bom, o problema nos diz que o aumento do comprimento tem que ficar no eixo horizontal, ou seja, esse será o nosso x; e o aumento de carga no eixo vertical, o nosso y. Portanto

F ⊥ = ( Y A l 0 ) ∆ l

Estabelecendo os valores da tabela, o nosso gráfico terá uma cara de

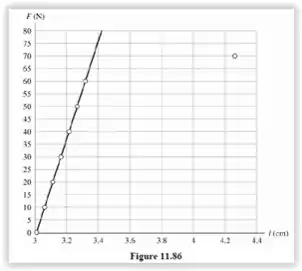
Passo 2

Vamos calcular agora o módulo de Young,

Y = l 0 F ⊥ A ∆ l

Y = l 0 π r 2 ( 60   N 3,32 - 3,02 × 10 - 2 m )

Y = l 0 π r 2 ( 60   N 3,32 - 3,02 × 10 - 2 m )

Y = l 0 π r 2 ( 2 × 10 4 N / m )

Y = 3,5   m π ( 0,35 × 10 - 3 ) 2 ( 2 × 10 4 N / m )

Logo,

Y = 1,8 × 10 11 P a

Passo 3

A tensão no ponto 3,34 cm, pode ser calculada por T = F ⊥ A . A carga total no limite proporcional é 60 N+20 N=80 N.

T = F ⊥ A = 80   N π ( 0,35 × 10 - 3 ) 2 = 2,1 × 10 8   P a

Resposta

a) gráfico.

b) Y = 1,8 × 10 11 P a

c)   T = 2,1 × 10 8   P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A figura mostra a curva tensão-deformação de um material. A escala do eixo das tensões é definida por s=300 , em unidades de 10 6N / m ² ². Determine (a) o módulo de Young e (b) o valor aproximado do
Um túnel de comprimento L=150m , altura H=7,2m , largura de 5,8m e teto plano deve ser construído a uma distância d=60m da superfície. O teto do túnel deve ser sustentado inteiramente por colunas quad
Na figura, um tijolo de chumbo repousa horizontalmente sobre os cilindros A e B . As áreas das faces superiores dos cilindros obedecem à relação A A = 2 A B ; os módulos de Young dos cilindros obedece
A figura mostra o gráfico tensão-deformação aproximado de um fio de teia de aranha, até o ponto em que se rompe com uma deformação de 2,00 . A escala do eixo das tensões é definida por a=0,12G N / m 2
A Figura mostra a curva tensão-deformação de um fio de alumínio que está sendo ensaiado em uma máquina que puxa as duas extremidades do fio em sentidos opostos. A escala do eixo das tensões é definida