Enunciado
Física - Young and Freedman - Vol 1- Ed: 14º - Capítulo 3.Problemas - Ex. 81
Um foguete projetado para colocar pequenas cargas em órbita é conduzido a uma altura de 12,0 km acima do nível do mar por uma aeronave convertida. Quando a aeronave está voando em linha reta com velocidade constante de 850 km/h, o foguete é liberado. Depois de soltá-lo, a aeronave mantém as mesmas altitude e velocidade e continua a voar em linha reta. O foguete cai durante um pequeno intervalo, depois do qual seu motor é acionado. Com o motor funcionando, o efeito combinado da gravidade e da força motriz produz uma aceleração constante de módulo 3,0g dirigida para cima e formando um ângulo de 30,0º com a horizontal. Por razões de segurança, o foguete deve permanecer pelo menos a uma distância de 1,0 km à frente da aeronave quando ele sobe até atingir a altura dela. Sua tarefa é calcular o intervalo mínimo da queda do foguete antes de seu motor ser acionado. Despreze a resistência do ar. Sua solução deve incluir: (i) um diagrama que mostre as
trajetórias do voo do foguete e da aeronave, identificadas mediante seus respectivos vetores para a velocidade e a aceleração em diversos pontos; (ii) um gráfico xt que mostre os movimentos do foguete e da aeronave; e (iii) um gráfico yt que mostre os movimentos do foguete e da aeronave. Nos diagramas e nos gráficos, indique o instante em que o foguete é lançado, o instante em que o motor é acionado e o instante em que o foguete sobe atingindo a altura da aeronave.
Passo 1
O foguete tem dois períodos de movimento de aceleração constante.
Seja +y para cima. Durante a fase de queda livre, . Depois que os motores ligam, .
Seja t o tempo total desde que o foguete foi lançado e seja T o momento em que o foguete cai antes de o motor dar partida.
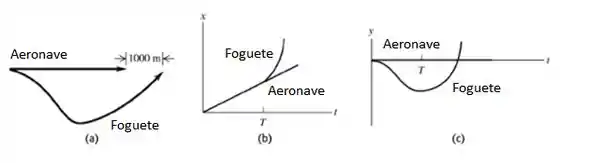
- O diagrama é dado na figura a.
- A posição x do avião é e a posição x do foguete é . Os gráficos dessas duas equações são esboçados na figura b.
- Se tomarmos y = 0 como a altitude do avião, então para o foguete. O avião tem y constante. Os gráficos são esboçados na figura b.
Em cada uma das figuras (de a até c), o foguete cai em t = 0 e o tempo T quando o motor é ligado e indicado.
Passo 2
Definindo y = 0 para o foguete, podemos resolver para t em termos de T:
Usando a fórmula quadrática para a variável , encontramos:
Ou
Agora, usando a condição de que , encontramos:
Ou
Portanto, .
Durante a fase de queda livre, o foguete e a aeronave têm a mesma coordenada x, mas o foguete move-se para baixo a partir da aeronave. Depois que os motores disparam, o foguete começa a se mover para cima e seu componente horizontal da velocidade começa a exceder o da aeronave
Resposta
.
Ver gráficos