Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 11.3 - Ex. 21
Um binário. Denomina-se conjugado ou binário duas forças de mesmo módulo, mesma direção e sentidos contrários aplicadas a dois pontos diferentes de um corpo. Duas forças antiparalelas de mesmo módulo são aplicadas sobre um eixo conforme indicado na Figura .
a) Qual deve ser a distância entre as forças sabendo-se que elas devem produzir um torque efetivo de em torno da extremidade esquerda do eixo?
b) O sentido do torque é igual ou contrário ao sentido da rotação dos ponteiros do relógio?
c) Repita os itens (a) e (b) considerando um pivô situado no ponto do eixo onde a força é aplicada.
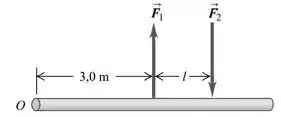
Passo 1
Fala, galera! Beleza? Vamos resolver essa questão!
O enunciado pediu pra gente (a) descobrir a distância entre as nossas forças e para que seja produzido um torque total de sobre o eixo , (b) verificar o sentido desse torque e (c) repetir os itens anteriores considerando um pivô situado no ponto do eixo onde a força é aplicada.
Pra isso, vamos desenhar um diagrama da corpo livre (DCL) do nosso sistema e usar as equações de equilíbrio, fazendo os somatório dos torque (com sentido anti-horário positivo) e analisar os nossos resultados.
Vamos lá!
Passo 2
Para a letra , precisamos descobrir a distância entre as nossas forças e para que seja produzido um torque total de sobre o eixo .
Desenhando um Diagrama do Corpo Livre, teremos:
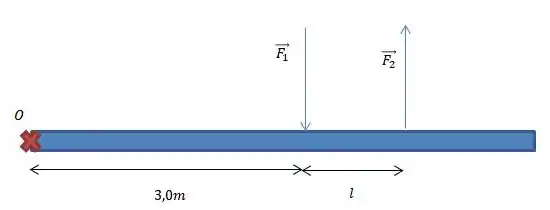
Calculando o somatório dos torques sobre o ponto e considerando o sentido anti-horário como positivo, teremos:
E como conhecemos o módulo das forças (, teremos:
E como queremos que o torque tenha módulo igual a , temos:
E assim, encontramos a distância necessária do binário para se ter o torque de sobre o eixo .
Passo 3
Para a letra b), precisamos indicar a direção do torque.
Como consideramos o sentido anti-horário como positivo na hora de calcular o torque e para encontrar o valor de usamos com um valor positivo, isso indica que o torque está no sentido anti-horário.
Isso é, o torque é no sentido contrário ao dos ponteiros do relógio.
(Isso também faz sentido só de olhar para o binário, percebe que o binário por si só, sem pensar na barra e no eixo , gera um torque no sentido anti-horário.)
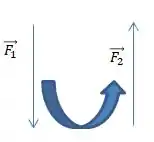
Passo 4
Agora, para a letra , precisamos repetir a letra e , isso é encontrar a distância e o sentido do torque para o caso de se ter um pivô no ponto onde a força é aplicada.
Portanto, agora não vamos mais calcular o torque sobre o ponto e sim sobre o pivô, afinal é ao redor dele que a barra irá girar com esse torque agora.
Fazendo o DCL, teremos:
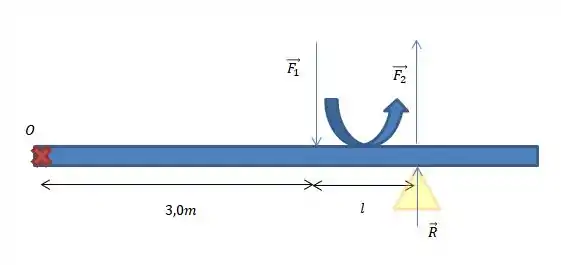
E fazendo o torque resultante sobre o pivô, e novamente considerando o sentido anti-horário como positivo, teremos:
Apenas a força irá gerar torque nesse caso, pois as forças e de reação estão no ponto aonde estamos calculando o torque.
Como queremos que o torque seja , teremos:
E assim como na letra , pelas nossas considerações esse torque gerado é no sentido contrário ao dos ponteiros do relógio.
Valeu, galera! Até a próxima! 😉
Resposta
- Contrário aos ponteiros do relógio.
- A mesma resposta que os itens e .