Enunciado

Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 11.3 - Ex. 9

Uma barra uniforme de e é suspensa horizontalmente por dois cabos verticais presos em cada extremidade. O cabo pode suportar uma tensão máxima de e o cabo pode suportar até . Você deseja colocar um pequeno peso sobre essa barra.

a) Qual é o peso máximo que você pode colocar sem romper qualquer dos dois cabos

b) em que ponto você deve colocar esse peso?

Passo 1

Fala, galera! Beleza? Vamos resolver essa questão!

O problema diz que uma barra é sustentada por dois cabos e nos dá a tensão que cada um suporta. É justamente o somatório dessas tensões dos cabos que anularam com a força peso da barra mais o objeto. Se essa força peso for maior, a corda arrebenta. Olha o esqueminha:

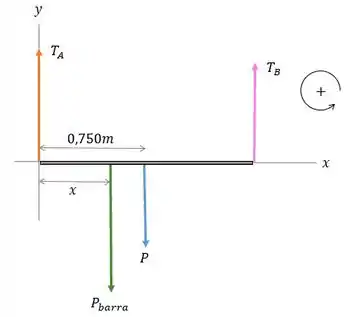
Nós precisamos aplicar as condições de equilíbrio à barra. E definir cada tensão igual ao seu valor máximo.

Pra isso, vamos deixar o cabo na extremidade esquerda. E vamos tomar o eixo na extremidade esquerda da barra e seja a distância do peso deste extremo, ok?

Vamos lá!

Passo 2

a) Vamos aplicar para que possamos encontrar o peso máximo que você pode colocar sem romper, então:

Somando as forças verticais do nosso sistema, temos:

E substituindo os valores do enuciado, ficamos com:

Passo 3

b) Agora vamos aplicar para sabermos em que ponto podemos aplicar esse peso. Pra isso vou escolher como centro de rotação a ponta esquerda da barra e nesse ponto vamos ter que:

Então, somando os torques do sistema, isso implica que:

Lembra que tomamos como referência . Dessa forma, temos que:

Logo, o peso deve ser colocado da extremidade esquerda da barra.

Valeu, galera! Até a próxima! 😉

Resposta

da extremidade esquerda barra

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Quando o pé de um corredor atinge o chão, a força de cisalhamento atuando sobre um solado de 8,0m m de espessura é como a mostrada na Figura 12-46. Se a força de 25N é distribuída sobre uma área de 15

Um cilindro, de massa M e raio R , rola até um degrau de altura h , como mostrado na figura. Quando uma força horizontal de magnitude F é aplicada no topo do cilindro, este permanece em repouso. (a) D

A Figura 12-62 mostra uma prancha homogênea, de 20 cm de comprimento, sobre um cilindro de 4,00 cm de raio. A massa da prancha é 5,0 kg e a do cilindro é 8,0 kg. O coeficiente de atrito estático entre

Um cubo maciço de aresta a, equilibrado sobre um cilindro de diâmetro d, está em equilíbrio instável se d ≪ a (Figura 12-64), e está em equilíbrio estável se d ≫ a . O cubo não escorrega sobre o cilin

Duas esferas maciças e polidas (sem atrito), de raio r, são colocadas dentro de um cilindro de raio R, como na Figura 12-63. A massa de cada esfera é m. Determine a força exercida pela base do cilindr