Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 11.3 - Ex. 11
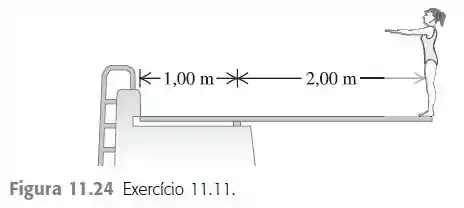
Uma prancha de trampolim com 3,0 m de comprimento é suportada em um ponto situado a 1,0m de uma de suas extremidades, e uma mergulhadora pesando 500 N está em pé na outra extremidade (Figura 11.24). A prancha possui seção reta uniforme e pesa 280 N. Calcule a) a força exercida sobre o ponto de suporte; b) a força na extremidade da esquerda.
Passo 1
Eaee, belezinha?? Bom... o enunciado nos diz que uma prancha de trampolim com de comprimento é suportada em um ponto situado a de uma de suas extremidades, e uma mergulhadora pesando está em pé na outra extremidade.
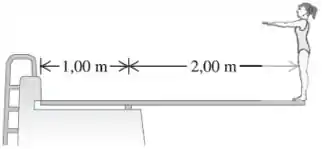
O enunciado nos diz que a prancha possui seção reta uniforme e pesa .
Queremos calcular a força exercida sobre o ponto de suporte e a força na extremidade da esquerda.
Para isso, precisaremos fazer um diagrama de corpo livre do sistema para estudarmos melhor as forças que estão atuando.
Também é importante perceber que o sistema da pessoa e do trampolim está em repouso, de modo que as duas condições de equilíbrio se aplicam: .
Essas duas condições são o somatório das forças e dos torques atuantes no sistema, respectivamente.
Passo 2
Vamos esboçar o diagrama do corpo livre para a prancha de mergulho, tomando a origem das coordenadas no lado esquerdo do tabuleiro (ponto A).
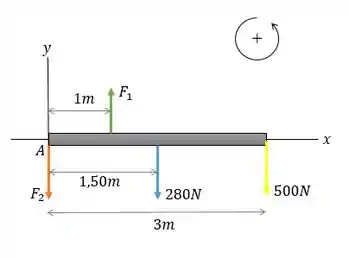
é a força aplicada no ponto de suporte.
a força no final que é pressionado.
Passo 3
- Então:
- E então, vamos aplicar a segunda lei de Newton no :
Sabemos que o torque é dado pelo produto entre a força pelo braço de alavanca.
Dessa forma, temos que:
Isso implica que:
Passo 4
Onde é a massa e é a aceleração.
E então: