Enunciado
Física - Young and Freedman - Vol 2- Ed: 12º - Capítulo 18.Problemas - Ex. 73
Uma função energia potencial geralmente usada para desrever a interação entre duas moléculas (Figura 18.8) é o potencial de Lennard- Jones com expoentes 6 e 12,
Onde r é a distancia entre os centros das moléculas e são constantes positivas. A força correspondente é dada pela equação 13.26. a) Faça gráficos de e por . b) Seja o valor de para qual , e o valor de r para o qual . Localize os pontos e nos seus gráficos. Qual desses valores representa a posição de equilíbrio entre as moléculas? c) calcule os valores de e em termos de e obtenha a razão . d) Se a distancia entre as moléculas for igual a (calculada no item (c)), qual seria o trabalho realizado para separá-las até uma distancia ?
Passo 1
A força correspondente a é dada pela equação 13.26:
Para chegar neste resultado é preciso integrar a energia potencial dada no enunciado do exercício.
Passo 2
a) Agora que obtemos a equação de e de , podemos plotar o gráfico delas.
O gráfico de é:
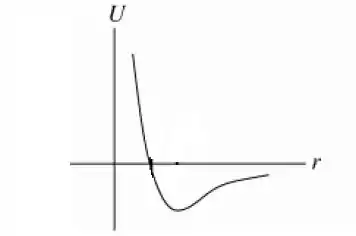
O gráfico de é:
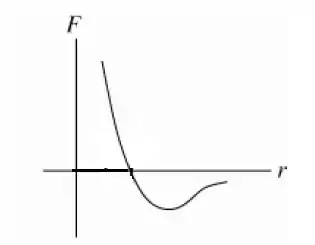
Passo 3
b) Supondo que seja o valor onde , desta forma teremos que é o ponto onde , ou seja, é onde a energia potencial é mínima.
Portanto a partículo estará em pois lá é onde se encontra o estado de menor energia.
Passo 4
c) Para resolver esse item vamos utilizar dois resultado que já conhecemos, que é o caso onde e .
A equação da energia potêncial é:
Se isso implica que:
Desta froma temos que é:
Pela equação da força, se , isso implica que:
Desta forma temos que é:
Portanto a razão vale:
Passo 5
d) O trabalho é igual a variação da energia potêncial, ou seja:
Se fizermos tendendo ao infinito temos que:
Portanto o trabalho é:
Resposta
b) A partícula está em
c)
d)