Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Halliday - Vol 4- Ed: 10º - Capítulo 39.5 - Ex. 54

A função de onda do estado quântico do átomo de hidrogêni cujo gráfico de pontos aparece na figura 39-21, para qual n = 2 e λ = m λ = 0 , é

ψ 200 r = 1 4 2 π a - 3 2 2 - r a e - r 2 a

onde a é o raio de Bohr e o índice de ψ ( r ) corresponde aos valores dos números quânticos n , λ e m λ . (a) Plote ψ 200 2 ( r ) em função de r e mostre que o gráfico é compatível com o gráfico de pontos da figura 39-21. (b) Mostre analiticamente que ψ 200 2 ( r ) passa por um máximo em r = 4 a . (c) Determine a densidade de probabilidade radial P 200 ( r ) para esse estado. (d) Mostre que

∫ 0 ∞ P 200 r d r = 1

e que, portanto, a expressão apresentada para a função de onda ψ 200 2 ( r ) está normalizada corretamente.

Passo 1

a) Antes de construir e analisar o gráfico precisamos elevar ψ 200 r ao quadrado.

ψ 200 2 r = 1 32 π a - 3 2 - r a 2 e - r a

O gráfico que obtemos é:

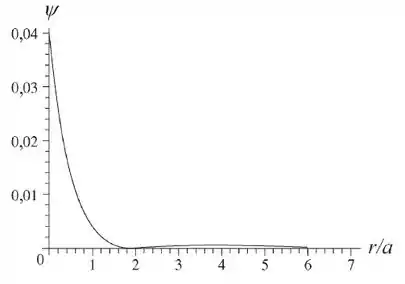
Foi plotado um gráfico de r / a ao invés de r apenas para facilitar a visualização do gráfico.

O gráfico de ψ 200 2 ( r ) mostrado acima deve ser comparado com o gráfico de pontos da figura 39-21. Note que o gráfico apresenta valores elevados na região entre r = 0 e r = 1,5 a , que corresponde à região com alta concentração de pontos em torno da origem na figura 39-21. Para valores maiores de r , existe uma região na qual os valores de ψ 200 2 ( r ) são muito pequenos, que corresponde ao espaço praticamente vazio da figura 39-21. Para valores ainda maiores de r , os valores de ψ 200 2 ( r ) voltam a aumentar, atingindo um segundo máximo, bem menor que o máximo central, em r = 4 a . A região em torno deste ponto corresponde ao anel com alta concentração de pontos da figura 39-21.

Passo 2

b) Para mostra analiticamente que ψ 200 2 ( r ) passa por um máximo em r = 4 a precisamos derivar e igualar a zero.

d ψ d r = - 1 32 r - 2 a r - 4 a a 6 π e - r a = 0

Desta forma para que essa expressão seja igual a zero r - 2 a = 0 ou r - 4 a = 0 , assim temos que r = 2 a ou r = 4 a .

Desta forma precisamos calcular a segunda derivada para saber qual dos dois valores é um máximo.

d 2 ψ d r 2 = - 1 32 2 r - 6 a - r - 2 a r - 4 a a e - r a

Se substituirmos r e dar um valor positivo temos um mínino e se der negativo temos um máximo, substituindo r = 4 a encontramos um valor negativo, logo temos que ele é um máximo.

Passo 3

c) A densidade de probabilidade radial é dada por:

P 200 r = 4 π r 2   ψ 200 2 r

Usando o valor de   ψ 200 2 r que encontramos no item (a):

P 200 r = r 2 8 a 3 2 - r a 2 e - r / a

Passo 4

d) Calculando a normalização da probabilidade encontrada no item (c):

∫ 0 ∞ P 200 r d r = ∫ 0 ∞ r 2 8 a 3 2 - r a 2 e - r a d r

Chamando x = r / a , temos que d x = ( 1 / a ) d r , substituindo na integral:

1 8 ∫ 0 ∞ x 2 2 - x 2 e - x d x = ∫ 0 ∞ ( x 4 - 4 x 3 + 4 x 2 ) e - x d x

1 8 4 ! - 4 3 ! + 4 ( 2 ! ) = 1

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para que valor do número quântico principal n o raio efetivo que aparece em um gráfico de pontos da densidade de probabilidade radial do átomo de hidrogênio é igual a 1,0m m ? Suponha que o valor de λ
12. Mostre que Φ ϕ = e i m l ϕ = Φ ( ϕ + 2 π ) (ou seja, mostre que Φ ( ϕ ) é periódica com período igual a 2 π ) se e somente se m l possuir valores restritos a 0 , ± 1 , ± 2 … (Sugestão: de acordo c
3. O momento angular de um elétron possui módulo igual a 4,716 ⋅ 10 - 34k g ⋅ m 2 / s . Qual é o número quântico do momento angular l desse elétron?
9. a ) Para a função de onda ψ r ,θ ,ϕ = R r Θ θ Φ ϕ onde a função Φ ϕ = A e i m ϕ , mostre que ψ 2 não depende de ϕ . b ) Qual deve ser o valor d A para que Φ ( ϕ ) satisfaça a condição de normalizaç
5. Calcule, em unidades de ℏ , o módulo do momento angular orbital máximo para um elétron em um átomo de hidrogênio em estados com um número quântico principal igual a 2 ,20 ,200 . Compare cada result