Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 3.Problemas - Ex. 80
Gotas de chuva. Quando a velocidade de um trem é de na direção leste, as gotas de chuva que caem verticalmente em relação à superfície terrestre deixam vestígios com inclinação de em relação à vertical, nas janelas do trem.
a) Qual o componente horizontal da velocidade de uma gota em relação à superfície terrestre? Em relação ao trem?
b) Qual o módulo da velocidade da gota em relação à superfície terrestre? Em relação ao trem?
Passo 1
Olá, tudo bem?
A ideia aqui é relacionar as velocidades relativas. Então vamos organizar os dados.
Temos três velocidades:
- A velocidade do trem relativa à Terra : na direção leste ;
- A velocidade da chuva em relação à Terra : verticalmente para baixo ;
- E por fim a velocidade relativa da chuva nas janelas do trem : em relação à vertical.
Podemos fazer um diagrama vetorial para visualizar melhor essas velocidades:
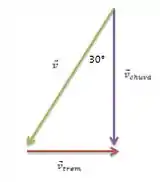Pelo diagrama dá pra gente ver que a velocidade das gotas de chuva em relação ao trem é uma subtração vetorial das velocidades da chuva (vertical, em roxo) e da velocidade do trem (horizontal, em vermelho). Assim, vetorialmente:
Ou, a velocidade da chuva em relação à Terra é a soma vetorial das outras duas:
Beleza?
Passo 2
- A letra a) pede a componente horizontal da velocidade de uma gota em relação à superfície terrestre e ao trem.
- Agora o problema nos pede o módulo das velocidades.
A velocidade das gotas em relação à Terra de chuva é vertical para baixo, e não possui componente horizontal. Então essa componente é zero.
Já em relação ao trem, para essa conta fechar, a componente horizontal de deve ser igual ao oposto do vetor , certo?
Então:
Tranquilo até aqui?
Passo 3
Primeiro vamos calcular o módulo da velocidade das gotas em relação à Terra . Pelo nosso diagrama, podemos formar um triângulo retângulo, onde podemos relacionar a tangente de com as componentes verticais (o que queremos) com a componente horizontal (velocidade do trem, que temos).
Achou difícil visualizar? Então vou simplificar girando aquele triângulo pra você ver melhor:
Sacou?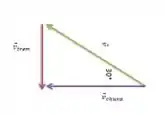
Com isso, temos que,
Substituindo os valores,
Show?
Passo 3
Por fim queremos o módulo da velocidade da gota em relação ao trem. Usando o mesmo triângulo do desenho do passo anterior, agora queremos saber o tamanho em verde. O módulo de vai ser nossa hipotenusa, a velocidade do trem vai ser nosso cateto oposto e a função que une isso tudo é o seno do ângulo, que é . Agora é só partir pra conta:
Isolando do lado esquerdo:
Certo? Vamos pra próxima questão? Responde Aí!
